题目内容
15.已知f(x)=ax2+bx+c(a>0),y=f(x)-x的零点为x1,x2,且0<x1<x2<$\frac{1}{a}$.(1)当x∈(0,x1),求证:x<f(x)<x1.
(2)若x=x0为y=f(x)的对称轴,求证:x0<$\frac{{x}_{1}}{2}$.
分析 (1)可以构造一个函数,然后利用做差的方法进行,然后判断差的符号即可;
(2)将对称轴用x1,x2表示出来,然后与$\frac{{x}_{1}}{2}$比较即可,注意性质的运用.
解答 证明:(1)令F(x)=f(x)-x,
因为x1,x2是方程f(x)-x=0的根,
所以F(x)=a(x-x1)(x-x2),且a>0,
当x∈(x1,x2)时,由x1<x<x2得(x-x1)(x-x2)<0,又a>0,
所以F(x)=a(x-x1)(x-x2)<0,即f(x)<x.
而x1-f(x)=x1-[x+F(x)]=x1-x+a(x1-x)(x-x2)=(x1-x)[1+a(x-x2)].
因为0<x1<x2<$\frac{1}{a}$,
所以x1-x<0,1+a(x-x2)=1+ax-ax2>1-ax2>0,
得x-f(x)<0,
由此得x1<f(x)<x.
(2)由(1)知f(x)=F(x)+x=x+a(x-x1)(x-x2)
=ax2+[1-a(x1+x2)]x+ax1x2
由x0=-$\frac{b}{2a}$=$\frac{a({x}_{1}+{x}_{2})-1}{2a}$=$\frac{a{x}_{2}-1}{2a}$+$\frac{{x}_{1}}{2}$,
因为ax2<1,所以$\frac{a{x}_{2}-1}{2a}$+$\frac{{x}_{1}}{2}$<$\frac{{x}_{1}}{2}$,
即x0<$\frac{{x}_{1}}{2}$.
点评 本题考查了二次函数与二次不等式、方程的根之间的关系,要注意将函数的性质与方程的根结合函数的图象有机结合起来.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知函数f(x)=x2-cosx,则$f(\frac{3}{5}),f(0),f(-\frac{1}{2})$的大小关系是( )
| A. | $f(0)<f(\frac{3}{5})<f(-\frac{1}{2})$ | B. | $f(0)<f(-\frac{1}{2})<f(\frac{3}{5})$ | C. | $f(\frac{3}{5})<f(-\frac{1}{2})<f(0)$ | D. | $f(-\frac{1}{2})<f(0)<f(\frac{3}{5})$ |
3.下列程序框图的功能是寻找使2×4×6×8×…×i>2015成立的i的最小正整数值,则输出框中应填( )


| A. | 输出i-2 | B. | 输出i-1 | C. | 输出i | D. | 输出i+1 |
20.若a、b、c∈R,a>b,则下列不等式成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a2>b2 | C. | $\frac{a}{{c}^{2}+1}$>$\frac{b}{{c}^{2}+1}$ | D. | |a|>|b| |
7.已知F是抛物线C:y2=4x的焦点,过点F的直线交抛物线C与A、B两点,且|AB|=6,则弦AB中点的横坐标为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 无法确定 |
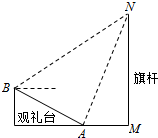 2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.
2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.