题目内容
11.若圆锥的侧面展开图是半径为2、圆心角为90°的扇形,则这个圆锥的全面积是$\frac{5}{4}π$.分析 根据圆锥的侧面积等于扇形的面积,再求出底面圆的面积,即可求出圆锥的表面积.
解答 解:∵圆锥的侧面展开图是圆心角为90°、半径为2的扇形,
∴圆锥的侧面积等于扇形的面积=$\frac{90×π×{2}^{2}}{360}$=π,
设圆锥的底面圆的半径为r,则
∵扇形的弧长为π,
∴2πr=π,
∴r=$\frac{1}{2}$,
∴底面圆的面积为$\frac{1}{4}π$,
∴圆锥的表面积为$π+\frac{1}{4}π$=$\frac{5}{4}π$,
故答案为:$\frac{5}{4}π$
点评 此题主要考查了圆锥的计算,根据圆锥的侧面积等于扇形的面积得出答案是解决问题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
1.已知数列{an}的通项公式为${a_n}={2^{5-n}}$,数列{bn}的通项公式为bn=n+k,设${c_n}=\left\{\begin{array}{l}{b_n},{a_n}≤{b_n}\\{a_n},{a_n}>{b_n}\end{array}\right.$,若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是( )
| A. | -5≤k≤-4 | B. | -4≤k≤-3 | C. | -5≤k≤-3 | D. | k=-4 |
2.设i为虚数单位,则|1-i|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
3.下列程序框图的功能是寻找使2×4×6×8×…×i>2015成立的i的最小正整数值,则输出框中应填( )
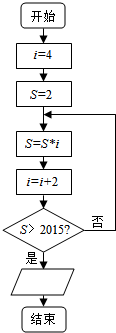

| A. | 输出i-2 | B. | 输出i-1 | C. | 输出i | D. | 输出i+1 |
20.若a、b、c∈R,a>b,则下列不等式成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a2>b2 | C. | $\frac{a}{{c}^{2}+1}$>$\frac{b}{{c}^{2}+1}$ | D. | |a|>|b| |
