题目内容
(本小题满分12分)已知函数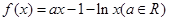 .
.
(Ⅰ)讨论函数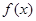 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数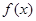 在
在 处取得极值,对
处取得极值,对 恒成立,求实数
恒成立,求实数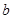 的取值范围.
的取值范围.
(Ⅰ)当 时
时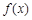 在
在 上没有极值点,当
上没有极值点,当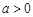 时,
时,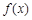 在
在 上有一个极值点(Ⅱ)
上有一个极值点(Ⅱ)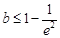
解析试题分析:(Ⅰ)显然函数的定义域为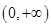 .
.
因为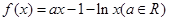 ,所以
,所以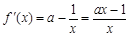 ,
,
当 时,
时, 在
在 上恒成立,函数
上恒成立,函数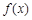 在
在 单调递减,
单调递减,
∴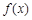 在
在 上没有极值点; ……3分
上没有极值点; ……3分
当 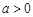 时,由
时,由 得
得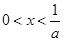 ,由
,由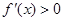 得
得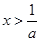 ,
,
∴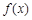 在
在 上递减,在
上递减,在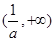 上递增,即
上递增,即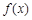 在
在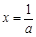 处有极小值.
处有极小值.
∴当 时
时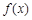 在
在 上没有极值点,当
上没有极值点,当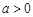 时
时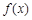 在
在 上有一个极值点.……6分
上有一个极值点.……6分
(Ⅱ)∵函数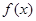 在
在 处取得极值,由(Ⅰ)结论知
处取得极值,由(Ⅰ)结论知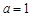 ,
,
∴ , ……8分
, ……8分
令 ,所以
,所以 ,
,
令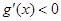 可得
可得 在
在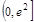 上递减,令
上递减,令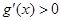 可得
可得 在
在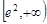 上递增, ……10分
上递增, ……10分
∴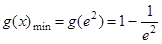 ,即
,即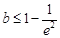 . ……12分
. ……12分
考点:本小题主要考查函数的求导、函数的单调性、函数的极值最值和恒成立问题,考查学生分析问题、解决问题的能力和分类讨论思想的应用以及运算求解能力.
点评:导数是研究函数问题的有力工具,常常用来解决函数的单调性、极值、最值等问题.对于题目条件较复杂,设问较多的题目审题时,应该细致严谨,将题目条件条目化,一一分析,细心推敲.对于设问较多的题目,一般前面的问题较简单,问题难度阶梯式上升,先由条件将前面的问题正确解答,然后将前面问题的结论作为后面问题解答的条件,注意问题之间的相互联系,使问题化难为易,层层解决.

练习册系列答案
相关题目
 .(Ⅰ) 求
.(Ⅰ) 求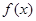 在
在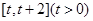 上的最小值;(Ⅱ) 若存在
上的最小值;(Ⅱ) 若存在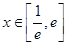 (
( 是常数,
是常数, )使不等式
)使不等式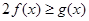 成立,求实数
成立,求实数 的取值范围;
的取值范围;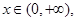 都有
都有 成立.
成立. ,其中
,其中 是自然常数,
是自然常数,
 时, 研究
时, 研究 的单调性与极值;
的单调性与极值;  ;
; - 2的极值.
- 2的极值. ,在
,在 与
与 时,都取得极值。
时,都取得极值。 的值;
的值; 都有
都有 恒成立,求c的取值范围。
恒成立,求c的取值范围。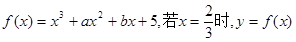 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3. 的解析式;
的解析式; 在
在 上的最大值和最小值.
上的最大值和最小值.
 是
是 的一个极值点.
的一个极值点. 时,
时, 恒成立,求
恒成立,求 的取值范围。
的取值范围。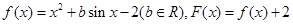 ,且对于任意实数
,且对于任意实数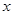 ,恒有
,恒有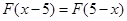 .
. 的解析式;
的解析式;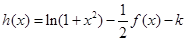 有几个零点?
有几个零点?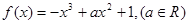
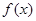 的图象上横坐标为
的图象上横坐标为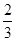 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;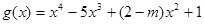 的图象与函数
的图象与函数