题目内容
(本小题满分12分)
已知函数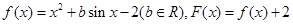 ,且对于任意实数
,且对于任意实数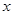 ,恒有
,恒有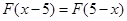 .
.
(1)求函数 的解析式;
的解析式;
(2)函数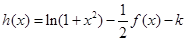 有几个零点?
有几个零点?
(1) .
.
(2)
 时,无零点;
时,无零点; 或
或
 时,有两个零点;
时,有两个零点;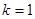 时有三个零点;
时有三个零点; 时,有四个零点.
时,有四个零点.
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
(本小题满分12分)
已知函数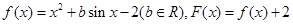 ,且对于任意实数
,且对于任意实数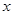 ,恒有
,恒有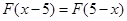 .
.
(1)求函数 的解析式;
的解析式;
(2)函数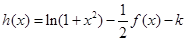 有几个零点?
有几个零点?
(1) .
.
(2)
 时,无零点;
时,无零点; 或
或
 时,有两个零点;
时,有两个零点;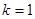 时有三个零点;
时有三个零点; 时,有四个零点.
时,有四个零点.
解析

 名校课堂系列答案
名校课堂系列答案