题目内容
(本小题满分12分)求函数f(x)= - 2的极值.
- 2的极值.
当x=-1时函数有极小值为-3;当x=1时函数有极大值为-1.
解析试题分析:先求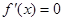 ,然后列表,再根据左正右负为极大值,左负右正为极小值,可求出极值.
,然后列表,再根据左正右负为极大值,左负右正为极小值,可求出极值.
由于函数f(x)的定义域为R ---------------- 2 分
---------------- 2 分
f'(x)=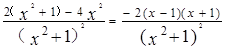 ----------- 6 分
----------- 6 分
令f'(x)=0得x=-1或x=1列表:
------------- 8 分x (-∞,-1) -1 (-1,1) 1 (1, ∞) f' (x) - 0 + 0 - f(x) ↘ 极小值 ↗ 极大值 ↘
由上表可以得到
当x=-1时函数有极小值为-3;当x=1时函数有极大值为-1. --------- 12分
考点:导数在求极值中的应用.
点评:掌握极大值与极小值的判断方法是解决本小题的关键.判断方法是极值点左正右负为极大值点;极值点的左负右正为极小值点.

练习册系列答案
相关题目
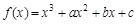 ,过曲线
,过曲线 上的点
上的点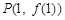 的切线方程为
的切线方程为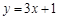
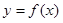 在
在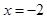 时有极值,求
时有极值,求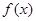 的表达式;
的表达式;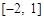 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.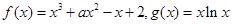
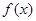 的单调递减区间为
的单调递减区间为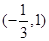 ,求函数
,求函数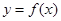 的图像过点
的图像过点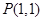 的切线方程;
的切线方程;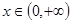 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.  ,曲线
,曲线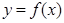 过点
过点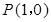 ,且在点
,且在点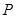 处的切线斜率为2.
处的切线斜率为2.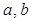 的值;
的值;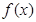 的极值点;
的极值点;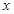 ,不等式
,不等式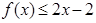 是否恒成立,若成立,请证明;若不成立,请说明理由。
是否恒成立,若成立,请证明;若不成立,请说明理由。
 ,试确定函数
,试确定函数 的单调区间;
的单调区间; ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;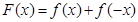 ,求证:
,求证: .
. 

 时,不等式
时,不等式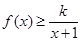 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围; .
.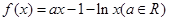 .
.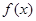 在定义域内的极值点的个数;
在定义域内的极值点的个数; 处取得极值,对
处取得极值,对 恒成立,求实数
恒成立,求实数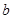 的取值范围.
的取值范围. 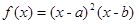 (
(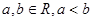 ).
).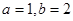 时,求曲线
时,求曲线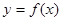 在点
在点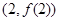 处的切线方程;
处的切线方程; 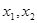 是
是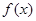 的两个极值点,
的两个极值点,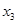 是
是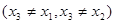 .证明:存在实数
.证明:存在实数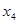 ,使得
,使得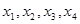 按某种顺序排列后构成等差数列,并求
按某种顺序排列后构成等差数列,并求 。
。 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数 的取值范围;
的取值范围;