题目内容
【题目】如图,圆O为△ABC的外接圆,过点C作圆O的切线交AB的延长线于点D,∠ADC的平分线交AC于点E,∠ACB的平分线交AD于点H. 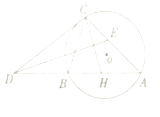
(1)求证:CH⊥DE;
(2)若AE=2CE.证明:DC=2DB.
【答案】
(1)证明:如图,
设DE与BC交于点F,则∠CFE=∠CDF+∠DCF,∠DEC=∠EDA+∠DAE,
因为DC为圆O的切线,
所以∠DCF=∠DAE,
又因DE为∠ADC的平分线,
所以∠CDF=∠EDA,
所以∠DEC=∠CFE
即∠CEF=∠CFE,所以△CFE为等腰三角形,
又因CH为∠ACB的平分线,所以CH⊥EF,
即CH⊥DE
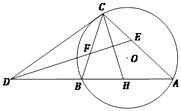
(2)证明:因DC为圆O的切线,
所以DC2=DBDA,
又因DE为∠ADC的平分线,AE=2CE,
所以 ![]() ,所以
,所以 ![]() =2,
=2,
即DC=2DB
【解析】(1)证明∠CEF=∠CFE,所以△CFE为等腰三角形,又因CH为∠ACB的平分线,所以CH⊥EF,即可证明CH⊥DE;(2)证明DC2=DBDA,因DE为∠ADC的平分线,AE=2CE.即可证明:DC=2DB.

练习册系列答案
相关题目