Question

【题目】已知首项为﹣6的等差数列{an}的前7项和为0，等比数列{bn}满足b3=a7 ， |b3﹣b4|=6．
（1）求数列{bn}的通项公式；
（2）是否存在正整数k，使得数列{ }的前k项和大于 ？并说明理由．

Answer 1

【答案】
（1）解：设等差数列{an}的公差为d，前n项Sn，a1=﹣6，

由S7=0，即7a1+ ×d=0，解得：d=2，

∴an=a1+（n﹣1）d=﹣6+（n﹣1）×2=2n﹣8，

设等比数列{bn}的公比为q，则由b3=a7=6，由|b3﹣b4|=6，即，|6﹣b4|=6．

∴b4=12或b4=0，

又∵{bn}为等比数列，

∴b4=12

∴q=2，

∴bn=b3qn﹣3=6×2n﹣3=3×2n﹣2，

数列{bn}的通项公式bn=3×2n﹣2

（2）解： ，

数列{ }是以 为首项，以 为公比的等比数列，

数列{ }的前k项和Tk= = （1﹣ ），

∴Tk＜ ，又∵ ＜ ，

∴不存在正整数k，使得数列{ }的前k项和大于

【解析】（1）由题意可知：7a1+ ×d=0，求得d=2，即可求得an=2n﹣8，则b3=a7=6，则|6﹣b4|=6．求得b4=12则q= =2，由等比数列的性质可知：bn=b3qn﹣3 ， 即可求得数列{bn}的通项公式；（2） ，数列{ }是以 为首项，以 为公比的等比数列，Tk= = （1﹣ ），则Tk＜ ， ＜ ，不存在正整数k，使得数列{ }的前k项和大于 ．
【考点精析】通过灵活运用数列的前n项和和数列的通项公式，掌握数列{an}的前n项和sn与通项an的关系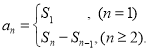；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式即可以解答此题．