Question

【题目】设圆的圆心在轴上，并且过两点.

(1)求圆的方程；

(2)设直线与圆交于两点，那么以为直径的圆能否经过原点，若能，请求出直线的方程；若不能，请说明理由.

Answer 1

【答案】(1) (2) 或.

【解析】试题分析：（1）圆的圆心在的垂直平分线上，又的中点为， ，∴的中垂线为.∵圆的圆心在轴上，∴圆的圆心为，因此，圆的半径，（2）设M,N的中点为H，假如以为直径的圆能过原点，则.，设是直线与圆的交点，将代入圆的方程得： .∴.∴的中点为.代入即可求得，解得.再检验即可

试题解析：

(1)∵圆的圆心在的垂直平分线上，

又的中点为， ，∴的中垂线为.

∵圆的圆心在轴上，∴圆的圆心为，

因此，圆的半径，

∴圆的方程为.

(2)设是直线与圆的交点，

将代入圆的方程得： .

∴.

∴的中点为.

假如以为直径的圆能过原点，则.

∵圆心到直线的距离为，

∴.

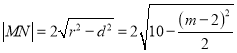∴，解得.

经检验时，直线与圆均相交，

∴的方程为或.