Question

【题目】已知四棱柱ABCD﹣A1B1C1D1的底面ABCD为正方形，AA1⊥AC，M、N分别为棱AA1、CC1的中点．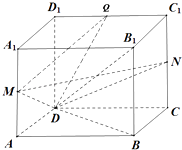

（1）求证：直线MN⊥平面B1BD；
（2）已知AA1=AB，AA1⊥AB，取线段C1D1的中点Q，求二面角Q﹣MD﹣N的余弦值．

Answer 1

【答案】
（1）

证明：∵四棱柱ABCD﹣A1B1C1D1的底面ABCD为正方形，AA1⊥AC，

∵M、N分别为棱AA1、CC1的中点，

∴MN∥AC，

∵在正方形ABCD中，AC⊥BD，

∴MN⊥BD，

∵BB1⊥AC，

∴MN⊥BB1，

∵BB1∩BD=B，

∴MN⊥平面BB1D

（2）

证明：∵AA1⊥AB，

∴四棱柱ABCD﹣A1B1C1D1为正方体，

以D为坐标原点，DA，DC，DD1所在直线分别为x轴、y轴、z轴，如图建立直角坐标系，

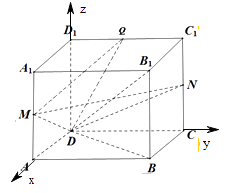
设棱长为2，

则M（2，0，1），D（0，0，0），N（0，2，1），Q（0，1，2），

易求得面MDN的一个法向量为 ，

则面QMD的一个法向量为 ，

则 ，

所以二面角Q﹣MD﹣N的余弦值为

【解析】（1）根据线面垂直的判定定理即可证明．（2）建立空间坐标系，求出平面的法向量，利用向量法进行求解即可．
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识，掌握一个平面过另一个平面的垂线，则这两个平面垂直．