Question

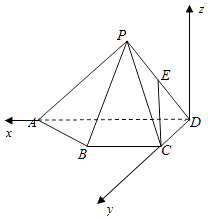
【题目】如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．
（Ⅰ）证明：CE∥平面PAB；
（Ⅱ）求直线CE与平面PBC所成角的正弦值．

Answer 1

【答案】证明：（Ⅰ）∵四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，
BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点，
∴以D为原点，DA为x轴，DC为y轴，过D作平面ABCD的垂线为z轴，建立空间直角系，
设PC=AD=2DC=2CB=2，
则C（0，1，0），D（0，0，0），P（1，0，1），E（ ），A（2，0，0），B（1，1，0），
=（ ）， =（1，0，﹣1）， =（0，1，﹣1），
设平面PAB的法向量 =（x，y，z），
则 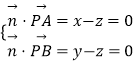，取z=1，得 =（1，1，1），
∵ = =0，CE平面PAB，
∴CE∥平面PAB．
解：（Ⅱ） =（﹣1，1，﹣1），设平面PBC的法向量 =（a，b，c），
则 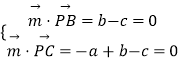，取b=1，得 =（0，1，1），
设直线CE与平面PBC所成角为θ，
则sinθ=|cos＜ ＞|= = = ．
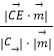∴直线CE与平面PBC所成角的正弦值为 ．

【解析】（Ⅰ）以D为原点，DA为x轴，DC为y轴，过D作平面ABCD的垂线为z轴，建立空间直角系，利用向量法能证明CE∥平面PAB．
（Ⅱ）求出平面PBC的法向量和 ，利用向量法能求出直线CE与平面PBC所成角的正弦值．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对空间角的异面直线所成的角的理解，了解已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则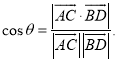．