Question

【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率为,它的一个顶点恰好是抛物线x2=4y的焦点.

(1)求椭圆C的方程;

(2)直线x=2与椭圆交于P,Q两点,P点位于第一象限,A,B是椭圆上位于直线x=2两侧的动点.

①若直线AB的斜率为,求四边形APBQ面积的最大值;

②当点A,B运动时,满足∠APQ=∠BPQ,问直线AB的斜率是否为定值,请说明理由.

Answer 1

【答案】（1）；（2）① ②

【解析】

(1)根据抛物线焦点，求得b，再由离心率和椭圆中a、b、c的关系求得a、c的值，进而得到椭圆的标准方程。

(2)设出A、B的坐标，联立直线与椭圆的方程，结合韦达定理求得x1+x2=-2t,x1x2=2t2-4；由直线x=2与椭圆交于P,Q两点可求得P,Q两点的坐标，则四边形APBQ的面积S=S△APQ+S△BPQ，即可得到面积的最大值；设出直线方程，联立椭圆方程，化简得到关于x的一元二次方程，利用韦达定理得到AB斜率的表达形式，即可得到斜率为定值。

(1)设椭圆C的方程为=1(a>b>0),由题意可得它的一个顶点恰好是抛物线x2=4y的焦点(0,),∴b=.

再根据离心率,求得a=2,

∴椭圆C的方程为=1.

(2)①设A(x1,y1),B(x2,y2),AB的方程为y=x+t,代入椭圆C的方程化简可得x2+2tx+2t2-4=0,由Δ=4t2-4(2t2-4)>0,求得-2<t<2.

由根与系数的关系可得x1+x2=-2t,x1x2=2t2-4.

在=1中,令x=2求得P(2,1),Q(2,-1),

∴四边形APBQ的面积S=S△APQ+S△BPQ=·PQ·|x1-x2|=×2×|x1-x2|=|x1-x2|=,

故当t=0时,四边形APBQ的面积S取得最大值为4.

②当∠APQ=∠BPQ时,PA,PB的斜率之和等于零,设PA的斜率为k,则PB的斜率为-k,PA的方程为y-1=k(x-2),把它代入椭圆C的方程化简可得(1+4k2)x2+8k(1-2k)x+4(1-2k)2-8=0,

∴x2+2=.

同理可得直线PB的方程为y-1=-k(x-2),x2+2=,

∴x1+x2=,x1-x2=.

∴AB的斜率k=

=

=

=.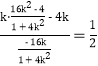