题目内容

2．已知向量$\overrightarrow{a}$=（1，k），$\overrightarrow{b}$=（-4，2），$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$垂直，那么k的值为（　　）
A．-2B．1C．-3或1D．2或3

分析 先求向量$\overrightarrow{a}+\overrightarrow{b}$的坐标，由$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}$垂直即可得到$（\overrightarrow{a}+\overrightarrow{b}）•\overrightarrow{a}=0$，进行数量积的坐标运算即可求出k．

解答 解：$\overrightarrow{a}+\overrightarrow{b}=（-3，k+2）$；
∵$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}$垂直；
∴$（\overrightarrow{a}+\overrightarrow{b}）•\overrightarrow{a}=-3+（k+2）k=0$；
解得k=1或-3．
故选C．

点评 考查向量坐标的加法运算，数量积运算，以及非零向量垂直的充要条件，解一元二次方程．

练习册系列答案
相关题目
12．若曲线y=x2-aln（x+1）在x=1处取极值，则实数a的值为（　　）
A．1B．2C．3D．4
13．已知$\overrightarrow{a}$=（2，λ），$\overrightarrow{b}$=（sin（2ωx-$\frac{π}{6}$），1），设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（$\frac{1}{2}$，1），若存在x∈（0，$\frac{π}{2}$），使$\overrightarrow{a}$⊥$\overrightarrow{b}$，求λ的取值范围．
10．若正数a，b满足$\frac{1}{a}$+$\frac{1}{b}$=1，则$\frac{1}{a-1}$+$\frac{4}{b-1}$的最小值为（　　）
A．3B．4C．5D．6
17．一个几何体的侧视图是边长为2的正三角形，正视图与俯视图的尺寸如图所示，则此几何体的体积为（　　）
A．12+2$\sqrt{3}$+3πB．12+3πC．$\sqrt{3}$π+2$\sqrt{3}$D．$\frac{\sqrt{3}π}{3}$+2$\sqrt{3}$
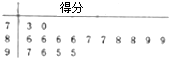7．钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所，被誉为深海中的翡翠．某学校就钓鱼岛有关常识随机抽取了16名学生进行测试，用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度，分数以小数点前的一位数字为茎，小数点后的一位数字为叶．
（1）指出这组数据的众数和中位数；
（2）若所得分数不低于9.5分，则称该学生对钓鱼岛“非常了解”．求从这16人中随机选取3人，求至多有1人“非常了解”的概率；
（3）以这16人的样本数据来估计该所学校学生的总体数据，若从该所学校（人数可视为很多）任选3人，记ξ表示抽到“非常了解”的人数，求ξ的分布列及数学期望．
14．已知f（x）定义在R上的函数，f′（x）是f（x）的导函数，若f（x）＞1-f′（x），且f（0）=2，则不等式exf（x）＞ex+1（其中e为自然对数的底数）的解集为（　　）
A．（0，+∞）B．（-∞，0）∪（1，+∞）C．（-1，+∞）D．（-∞，-1）∪（0，+∞）
11．已知函数f（x）为R上的增函数，函数图象关于点（3，0）对称，若实数x，y满足$f（{x^2}-2\sqrt{3}x+9）+f（{y^2}-2y）≤0$，则$\frac{y}{x}$的取值范围是[0，$\sqrt{3}$]．
12．给定函数①$y={x^{\frac{1}{2}}}$，②$y={log_{\frac{1}{2}}}（{x+1}）$，③y=|x+1|，④y=-2x+1，其中在区间（0，1）上单调递减的函数序号是（　　）
A．①②B．②③C．②④D．③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网