题目内容
17.某地举行了一场小型公车拍卖会,轿车拍卖成交了4辆,成交价格分别为3万元,x万元,7万元,9万元;货车拍卖成交了2辆,成交价格分别为7万元,8万元.总平均成交价格为7万元.(I)求该场拍卖会成交价格的中位数;
(Ⅱ)某人拍得两辆车,求拍得轿车、货车各一辆且总成交价格不超过14万元的概率.
分析 (I)先根据平均数求出x的值,再根据中位数的定义即可求出.
(Ⅱ)设轿车分别记为a3,a7,a8,a9,货车记为b7,b8,则从中任拍的两辆的基本事件有15种,拍得轿车、货车各一辆且总成交价格不超过14万元有3种,根据概率公式计算即可.
解答 解:(Ⅰ)由已知$\frac{1}{6}$(3+x+7+9+7+8)=7,解得x=8,
则成交价格的中位数为$\frac{7+8}{2}$=7.5.
(Ⅱ)设轿车分别记为a3,a7,a8,a9,货车记为b7,b8,则从中任拍的两辆的基本事件有a3a7,a3a8,a3a9,a3b7,a3a8,a7a8,a7a9,a7b7,a7a8,a8a9,a8b7,a8a8,
a9b7,a9a8,b7b8,共15种,
拍得轿车、货车各一辆且总成交价格不超过14万元基本事件有a3a7,a3a8,a7b7,共3种,
故拍得轿车、货车各一辆且总成交价格不超过14万元的概率$\frac{3}{15}$=$\frac{1}{5}$.
点评 本题考查了平均数中位数,以及古典概率的问题,属于基础题.

练习册系列答案
相关题目
5.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上为减函数,若$f({ln\frac{n}{m}})$+$f({ln\frac{m}{n}})$-2f(1)>0,则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是( )
| A. | (e,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
12.给定函数①$y={x^{\frac{1}{2}}}$,②$y={log_{\frac{1}{2}}}({x+1})$,③y=|x+1|,④y=-2x+1,其中在区间(0,1)上单调递减的函数序号是( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
2.执行如图的程序框图,如果输入a=4,那么输出的n的值为( )
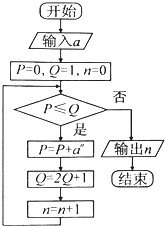

| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
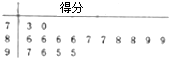 钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.
钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.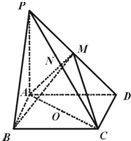 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.