题目内容
20.一个多边形的周长等于158cm,所有各边的长成等差数列,最大边的长等于44cm,公差等于3cm,求多边形的边数.分析 利用等差数列的通项及求和公式,建立方程,即可求多边形的边数.
解答 解:由题意可知:an=44,Sn=158,d=3
则Sn=$\frac{n({a}_{1}+44)}{2}$=158,an=a1+3(n-1)=44
即n(a1+44)=316 (1),a1=47-3n (2)
(2)代入(1),得3n2-91n+316=0
∴(3n-79)(n-4)=0,解得n=4
∴多边形的边数为4.
点评 本题考查等差数列的通项及求和公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
5.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上为减函数,若$f({ln\frac{n}{m}})$+$f({ln\frac{m}{n}})$-2f(1)>0,则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是( )
| A. | (e,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
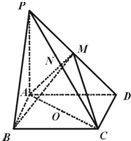 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.