题目内容
7．已知函数f（x）=|ax|-|x-a|（a＞0），若关于x的不等式f（x）＜0的解集中的整数恰有4个，则实数a的取值范围为（ ）| A． | $\frac{3}{4}$＜a≤$\frac{3}{2}$ | B． | $\frac{4}{3}$≤a＜$\frac{3}{2}$ | C． | $\frac{3}{2}$＜a≤2 | D． | $\frac{3}{2}$≤a＜2 |
分析 不等式f（x）＜0可化为|ax|＜|x-a|（a＞0），作函数y=|ax|与函数y=|x-a|的图象，结合图象可解得$\frac{a}{1-a}$＜x＜$\frac{a}{1+a}$；从而求得．
解答 解：不等式f（x）＜0可化为|ax|＜|x-a|（a＞0），
作函数y=|ax|与函数y=|x-a|的图象如下，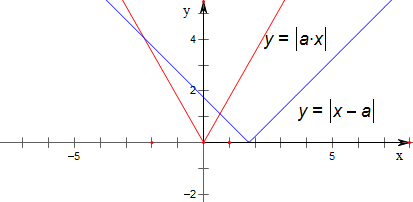
结合图象可知，a＞1，
故不等式化为
$\left\{\begin{array}{l}{-ax＜a-x}\\{x＜0}\end{array}\right.$或$\left\{\begin{array}{l}{ax＜a-x}\\{x≥0}\end{array}\right.$，
解得，$\frac{a}{1-a}$＜x＜0或0≤x＜$\frac{a}{1+a}$；
故$\frac{a}{1-a}$＜x＜$\frac{a}{1+a}$；
∵0＜$\frac{a}{1+a}$＜1，且关于x的不等式f（x）＜0的解集中的整数恰有4个，
∴4个整数为0，-1，-2，-3；
∴-4≤$\frac{a}{1-a}$＜-3，
解得，$\frac{4}{3}$≤a＜$\frac{3}{2}$；
故选：B．
点评 本题考查了绝对值不等式的解法与函数的图象与不等式的关系应用，属于中档题．
练习册系列答案
相关题目