题目内容
2.f(x)=|x2-2x-5|,且f(x)=a,方程有解,根据解的个数,得出a的取值范围.分析 方程f(x)=a的解的个数可看成函数f(x)=|x2-2x-5|与函数y=a的图象的交点的个数,从而结合图象求解即可.
解答 解:作函数f(x)=|x2-2x-5|的图象如下,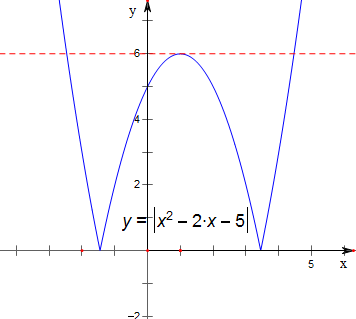
结合图象可知,
当方程f(x)=a有两个解时,a>6或a=0,
当方程f(x)=a有三个解时,a=6,
当方程f(x)=a有四个解时,0<a<6,
当方程f(x)=a没有解时,a<0.
点评 本题考查了方程的根与函数的图象的关系应用及数形结合的思想应用,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
7.已知函数f(x)=|ax|-|x-a|(a>0),若关于x的不等式f(x)<0的解集中的整数恰有4个,则实数a的取值范围为( )
| A. | $\frac{3}{4}$<a≤$\frac{3}{2}$ | B. | $\frac{4}{3}$≤a<$\frac{3}{2}$ | C. | $\frac{3}{2}$<a≤2 | D. | $\frac{3}{2}$≤a<2 |
12.要得到y=2sin(2x-$\frac{π}{3}$)的图象,只需把y=2sin(2x+$\frac{π}{4}$)的图象( )
| A. | 向右平移$\frac{7}{12}$π个单位 | B. | 向左平移$\frac{7}{24}$π个单位 | ||
| C. | 向右平移$\frac{7}{24}$π个单位 | D. | 向左平移$\frac{7}{12}$π个单位 |