题目内容
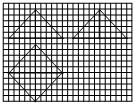 一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为
一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:三视图复原的几何体是正四棱锥,利用三视图的数据,求出几何体的体积即可.
解答:
解:三视图复原的几何体是底面为边长为5
的正方形,高为5正四棱锥,
所以几何体的体积为
×(5
)2×5=
故答案为:
.
| 2 |
所以几何体的体积为
| 1 |
| 3 |
| 2 |
| 250 |
| 3 |
故答案为:
| 250 |
| 3 |
点评:本题考查简单几何体的三视图,几何体的体积的求法,考查空间想象能力与计算能力.

练习册系列答案
相关题目
设a,b,c,d∈R,给出下列命题:
①若ac>bc,则a>b;
②若a>b,c>d,则a+c>b+d;
③若a>b,c>d,则ac>bd;
④若ac2>bc2,则a>b.
其中真命题的序号是( )
①若ac>bc,则a>b;
②若a>b,c>d,则a+c>b+d;
③若a>b,c>d,则ac>bd;
④若ac2>bc2,则a>b.
其中真命题的序号是( )
| A、①② | B、②④ |
| C、①②④ | D、②③④ |
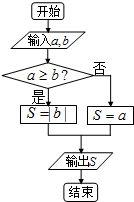 定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )
定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )| A、2 | B、-1 | C、4 | D、3 |
函数y=x2-1的值域是( )
| A、[-1,+∞) |
| B、R |
| C、[0,+∞) |
| D、[1,+∞) |
P:x≥3或x≤1,Q:x2-3x+2≥0,则“非P”是“非Q”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
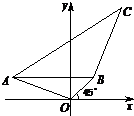 如图,在平面直角坐标系xOy中,已知点A(-3,1),直线OB的倾斜角为45°,且|OB|=
如图,在平面直角坐标系xOy中,已知点A(-3,1),直线OB的倾斜角为45°,且|OB|=