题目内容
方程x2+y2+2ax-by+c=0表示圆心为C（2，3），半径为3的圆，则a、b、c的值依次为（ ）
| A、2、6、4 |
| B、-2、6、4 |
| C、2、-6、4 |
| D、2、-6、-4 |
考点：圆的一般方程
专题：直线与圆
分析：由已知得
，由此能求出结果．
|
解答：
解：∵方程x2+y2+2ax-by+c=0表示圆心为C（2，3），半径为3的圆，
∴
，
解得a=-2，b=6，c=4．
故选：B．
∴
|
解得a=-2，b=6，c=4．
故选：B．
点评：本题考查圆的方程的应用，是基础题，解题时要注意圆的性质的合理运用．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
函数f（x）=
的零点是（ ）
| x3-x2 |
| x |
| A、-1 | B、0 | C、1 | D、0或-1 |
设a，b，c，d∈R，给出下列命题：
①若ac＞bc，则a＞b；
②若a＞b，c＞d，则a+c＞b+d；
③若a＞b，c＞d，则ac＞bd；
④若ac2＞bc2，则a＞b．
其中真命题的序号是（ ）
①若ac＞bc，则a＞b；
②若a＞b，c＞d，则a+c＞b+d；
③若a＞b，c＞d，则ac＞bd；
④若ac2＞bc2，则a＞b．
其中真命题的序号是（ ）
| A、①② | B、②④ |
| C、①②④ | D、②③④ |
在△ABC中，角A，B，C所对的边长分别为a，b，c，若∠C=120°，c=2a，则（ ）
| A、a＞b |
| B、a＜b |
| C、a=b |
| D、a与b的大小关系不能确定 |
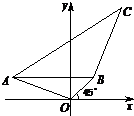如图，在平面直角坐标系xOy中，已知点A（-3，1），直线OB的倾斜角为45°，且|OB|=