题目内容
曲线y=
x3+
在点（2，4）处的切线方程是（ ）
| 1 |
| 3 |
| 4 |
| 3 |
| A、x+4y-4=0 |
| B、x-4y-4=0 |
| C、4x+y-4=0 |
| D、4x-y-4=0 |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：由原函数求得导函数，得到函数在x=2时的导数值，然后由直线方程的点斜式得答案．
解答：
解：由y=
x3+
，得y′=x2，
∴y′|x=2=4，
∴曲线y=
x3+
在点（2，4）处的切线方程是y-4=4（x-2），即4x-y-4=0．
故选：D．
| 1 |
| 3 |
| 4 |
| 3 |
∴y′|x=2=4，
∴曲线y=
| 1 |
| 3 |
| 4 |
| 3 |
故选：D．
点评：本题考查了利用导数研究过曲线上某点处的切线方程，过曲线上某点的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
相关题目
设a，b，c∈R+，那么三个数a+
，b+
，c+
（ ）
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、都不大于2 |
| B、都不小于2 |
| C、至少有一个不小于2 |
| D、至少有一个不大于2 |
函数f（x）=
的零点是（ ）
| x3-x2 |
| x |
| A、-1 | B、0 | C、1 | D、0或-1 |
设a1，d为实数，首项为a1，公差为d的等差数列{an}的前n项的和为Sn，满足S5S6=-15，则a1的取值范围是（ ）
A、（-∞，-2
| ||||
B、[2
| ||||
C、（-∞，-2
| ||||
D、[2
|
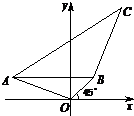如图，在平面直角坐标系xOy中，已知点A（-3，1），直线OB的倾斜角为45°，且|OB|=