题目内容
设a>0,b>0且a+b=1则
+
的最小值是( )
| 1 |
| a |
| 2 |
| b |
| A、2 | ||
| B、4 | ||
C、3+2
| ||
| D、6 |
考点:基本不等式
专题:不等式的解法及应用
分析:利用“乘1法”和基本不等式的性质即可得出.
解答:
解:∵a>0,b>0且a+b=1,
∴
+
=(a+b)(
+
)=3+
+
≥3+2
=3+2
,当且仅当b=
a=2-
取等号.
∴
+
的最小值是3+2
.
故选:C.
∴
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 2a |
| b |
|
| 2 |
| 2 |
| 2 |
∴
| 1 |
| a |
| 2 |
| b |
| 2 |
故选:C.
点评:本题考查了“乘1法”和基本不等式的性质,属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
直线y=2x+1与y轴的交点所组成的集合为( )
| A、{0,1} | ||
| B、{(0,1)} | ||
C、{-
| ||
D、{(-
|
P:x≥3或x≤1,Q:x2-3x+2≥0,则“非P”是“非Q”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
有一半径为4的圆,现将一枚直径为2的硬币投向其中(硬币与圆面有公共点就算是有效试验,硬币完全落在圆外的不计),则硬币完全落入圆内的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
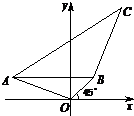 如图,在平面直角坐标系xOy中,已知点A(-3,1),直线OB的倾斜角为45°,且|OB|=
如图,在平面直角坐标系xOy中,已知点A(-3,1),直线OB的倾斜角为45°,且|OB|=