题目内容
10.设O为△ABC所在平面上一点,则下列说法中正确的有①③④(填上正确命题的序号)①若$\overrightarrow{OA}•\overrightarrow{OB}=\overrightarrow{OB}•\overrightarrow{OC}=\overrightarrow{OC}•\overrightarrow{OA}$,则O为△ABC的垂心;
②若$|\overrightarrow{OA}{|}^{2}+|\overrightarrow{BC}{|}^{2}$=$|\overrightarrow{OB}{|}^{2}+|\overrightarrow{CA}{|}^{2}$=$\overrightarrow{|OC}{|}^{2}+|\overrightarrow{AB}{|}^{2}$,则点O是△ABC的内心;
③若O在△ABC内部,且3$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,则$\frac{{S}_{△ABC}}{{S}_{△OBC}}$=$\frac{5}{3}$;
④若O在△ABC内部,且$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$=$\overrightarrow{0}$,则S△ABO:S△BCO:S△ACO=3:1;2.
分析 ①将已知向量等式变形,利用向量的运算法则化简,再利用向量垂直的充要条件判断出两个向量垂直得到两条线垂直,判断出O为垂心.
②根据向量的减法,利用数量积运算和题意代入式子进行化简,证出OC⊥AB,同理可得OB⊥AC,OA⊥BC,即证出O是△ABC的垂心.
③取BC的中点O,若O在△ABC内部,且3$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,OD=$\frac{5}{3}$AD,可得$\frac{{S}_{△ABC}}{{S}_{△OBC}}$=$\frac{5}{3}$;
④延长OB到点E,使得$\overrightarrow{OE}$=2$\overrightarrow{OB}$,分别以$\overrightarrow{OA}$,$\overrightarrow{OE}$为邻边作平行四边形OAFE,则$\overrightarrow{OA}$+2$\overrightarrow{OB}$=$\overrightarrow{OF}$,利用$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$=$\overrightarrow{0}$,可得$\overrightarrow{OF}$=3$\overrightarrow{OC}$,从而可得S△ABC=2S△AOB.同理可得:S△ABC=3S△AOC,S△ABC=6S△BOC.
解答 解:①若$\overrightarrow{OA}•\overrightarrow{OB}=\overrightarrow{OB}•\overrightarrow{OC}=\overrightarrow{OC}•\overrightarrow{OA}$,则($\overrightarrow{OA}$-$\overrightarrow{OC}$)•$\overrightarrow{OB}$=0,∴$\overrightarrow{CA}$⊥$\overrightarrow{OB}$,∴CA⊥OB,同理OA⊥BC,∴O是△ABC的垂心,正确;
②设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BC}$=$\overrightarrow{c}$-$\overrightarrow{b}$,$\overrightarrow{CA}$=$\overrightarrow{a}$-$\overrightarrow{c}$,$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{a}$.
由题可知,$|\overrightarrow{OA}{|}^{2}+|\overrightarrow{BC}{|}^{2}$=$|\overrightarrow{OB}{|}^{2}+|\overrightarrow{CA}{|}^{2}$=$\overrightarrow{|OC}{|}^{2}+|\overrightarrow{AB}{|}^{2}$,
∴|$\overrightarrow{a}$|2+|$\overrightarrow{c}$-$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{a}$-$\overrightarrow{c}$|2,化简可得$\overrightarrow{c}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,即($\overrightarrow{b}$-$\overrightarrow{a}$)•$\overrightarrow{c}$=0,
∴$\overrightarrow{OC}•\overrightarrow{AB}=0$,∴$\overrightarrow{AB}$⊥$\overrightarrow{OC}$,即OC⊥AB.同理可得OB⊥AC,OA⊥BC.∴O是△ABC的垂心,不正确;
③取BC的中点O,若O在△ABC内部,且3$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,OD=$\frac{5}{3}$AD,则$\frac{{S}_{△ABC}}{{S}_{△OBC}}$=$\frac{5}{3}$,正确;
④延长OB到点E,使得$\overrightarrow{OE}$=2$\overrightarrow{OB}$,分别以$\overrightarrow{OA}$,$\overrightarrow{OE}$为邻边作平行四边形OAFE.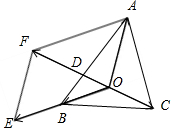
则$\overrightarrow{OA}$+2$\overrightarrow{OB}$=$\overrightarrow{OF}$,
∵$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$=$\overrightarrow{0}$,∴$\overrightarrow{OF}$=3$\overrightarrow{OC}$.
又$\overrightarrow{AF}$=2$\overrightarrow{OB}$,∴$\overrightarrow{DF}$=2$\overrightarrow{OD}$.∴$\overrightarrow{CO}$=$\overrightarrow{OD}$,∴S△ABC=2S△AOB.
同理可得:S△ABC=3S△AOC,S△ABC=6S△BOC.
∴S△ABO:S△BCO:S△ACO=3:1;2
故答案为:①③④.
点评 本题考查了向量在几何中应用,主要利用向量的线性运算以及数量积进行化简证明,特别证明垂直主要根据题意构造向量利用数量积为零进行证明.

 计算高手系列答案
计算高手系列答案| A. | p∧q | B. | ¬p∧¬q | C. | ¬p∧q | D. | p∧¬q |
| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(Ⅱ)若周六同一时间段车流量是25万辆,试根据(Ⅰ)求出的线性回归方程预测,此时PM2.5的浓度为多少(保留整数)?
(参考公式:$\hat b=\frac{{\sum_{i=1}^5{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^5{{{({x_i}-\overline x)}^2}}}},\overline y=\hat b•\overline x+\hat a$,参考数据:$\sum_{i=1}^5{x_i}=270,\sum_{i=1}^5{y_i}=370$)

| A. | 23 | B. | 24 | C. | 25 | D. | 26 |