题目内容
1.设函数f(x)=cos($\frac{π}{2}$-x)cosx-sin2(π-x)-$\frac{1}{2}$.(Ⅰ) 求函数f(x)的最小正周期和单调递增区间;
(Ⅱ) 若f(α)=$\frac{3\sqrt{2}}{10}$-1,且α∈($\frac{π}{8}$,$\frac{3π}{8}$),求f(α-$\frac{π}{8}$)的值.
分析 (Ⅰ)由条件利用三角恒等变换化简函数f(x)的解析式,再利用正弦函数的周期性和单调性得出结论.
(Ⅱ)由条件利用同角三角函数的基本关系、两角和差的三角公式求得$f(α-\frac{π}{8})$的值.
解答 解:(Ⅰ)∵$f(x)=sinxcosx-{sin^2}x-\frac{1}{2}$=$\frac{1}{2}(sin2x+cos2x)-1$=$\frac{{\sqrt{2}}}{2}sin(2x+\frac{π}{4})-1$,
∴f(x)的最小正周期为$T=\frac{2π}{2}=π$.
由$2kπ-\frac{π}{2}≤2x+\frac{π}{4}≤2kπ+\frac{π}{2}$,得$kπ-\frac{3π}{8}≤x≤kπ+\frac{π}{8}$,
∴f(x)的单调递增区间为$[kπ-\frac{3π}{8},kπ+\frac{π}{8}](k∈Z)$.
(Ⅱ)∵$f(α)=\frac{{\sqrt{2}}}{2}sin(2α+\frac{π}{4})-1=\frac{{3\sqrt{2}}}{10}-1$,∴$sin(2α+\frac{π}{4})=\frac{3}{5}$.
由$α∈(\frac{π}{8},\frac{3π}{8})$知$2α+\frac{π}{4}∈(\frac{π}{2},π)$,∴$cos(2α+\frac{π}{4})=-\frac{4}{5}$.
∴$f(α-\frac{π}{8})=\frac{{\sqrt{2}}}{2}sin[2(α-\frac{π}{8})+\frac{π}{4}]-1$=$\frac{{\sqrt{2}}}{2}sin[(2α+\frac{π}{4})-\frac{π}{4})]-1$
=$\frac{{\sqrt{2}}}{2}[sin(2α+\frac{π}{4})cos\frac{π}{4}-cos(2α+\frac{π}{4})sin\frac{π}{4}]-1$
=$\frac{{\sqrt{2}}}{2}×(\frac{3}{5}×\frac{{\sqrt{2}}}{2}+\frac{4}{5}×\frac{{\sqrt{2}}}{2})-1$=$-\frac{3}{10}$.
点评 本题主要考查三角函数的恒等变换及化简求值,正弦函数的周期性和单调性,属于中档题.

| A. | 0.5 | B. | 1.5 | C. | 2.5 | D. | 3.5 |
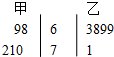
| A. | 甲、甲 | B. | 乙、甲 | C. | 甲、乙 | D. | 乙、乙 |
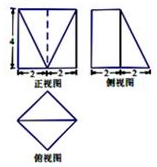 若一个几何体的三视图如图所示,则该几何体的体积是( )
若一个几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | $\frac{80}{3}$ | D. | $\frac{160}{3}$ |