题目内容
2.PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如下表:| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(Ⅱ)若周六同一时间段车流量是25万辆,试根据(Ⅰ)求出的线性回归方程预测,此时PM2.5的浓度为多少(保留整数)?
(参考公式:$\hat b=\frac{{\sum_{i=1}^5{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^5{{{({x_i}-\overline x)}^2}}}},\overline y=\hat b•\overline x+\hat a$,参考数据:$\sum_{i=1}^5{x_i}=270,\sum_{i=1}^5{y_i}=370$)
分析 (Ⅰ)根据公式求出b,a,可写出线性回归方程;
(Ⅱ)根据(Ⅰ)的性回归方程,代入x=25求出PM2.5的浓度.
解答 解:(Ⅰ)由条件可知$\overline{x}$=$\frac{1}{5}$(50+51+54+57+58)=54,$\overline{y}$=$\frac{1}{5}$(69+70+74+78+79)=74
$\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=4×5+3×4+3×4+4×5=64,$\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}$=50,
∴b=$\frac{64}{50}$=1.28,a=74-1.28×54=4.88,
故y关于x的线性回归方程是:y=1.28x+4.88;
(Ⅱ)当x=25时,y=1.28×25+4.88=36.88≈37,
∴可以预测此时PM2.5的浓度约为37.
点评 本题主要考查了线性回归分析的方法,包括用最小二乘法求参数,以及用回归方程进行预测等知识,考查了考生数据处理和运算能力.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
13.甲乙两位同学最近五次模考数学成绩茎叶图如图,则平均分数较高和成绩比较稳定的分别是( )
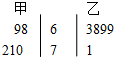
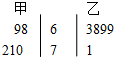
| A. | 甲、甲 | B. | 乙、甲 | C. | 甲、乙 | D. | 乙、乙 |
17.设i是虚数单位,则复数1-2i+3i2-4i3等于( )
| A. | -2-6i | B. | -2+2i | C. | 4+2i | D. | 4-6i |
7.函数f(x)为奇函数且f(3x+1)的周期为3,f(1)=-1,则f(2015)=( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
11.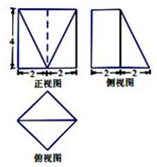 若一个几何体的三视图如图所示,则该几何体的体积是( )
若一个几何体的三视图如图所示,则该几何体的体积是( )
 若一个几何体的三视图如图所示,则该几何体的体积是( )
若一个几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | $\frac{80}{3}$ | D. | $\frac{160}{3}$ |