题目内容
15.在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似实数排序的定义,我们定义“点序”记为“>”:已知M(x1,y1)和N(x2,y2),M>N,当且仅当“x1>x2”或“x1=x2且y1>y2”.定义两点的“⊕”与“?”运算如下:M⊕N=(x1+x2,y1+y2),M?N=x1x2+y1y2则下面四个命题:①已知P(2015,2014)和Q(2014,2015),则P>Q;
②已知P(2015,2014)和Q(x,y),若P>Q,则x≤2015,且y≤2014;
③已知P>Q,Q>M,则P>M;
④已知P>Q,则对任意的点M,都有P⊕M>Q⊕M;
⑤已知P>Q,则对任意的点M,都有P?M>Q?M
其中真命题的序号为①③④(把真命题的序号全部写出)
分析 ①已知P(2015,2014)和Q(2014,2015),由于2015>2014,即可判定出正误;
②若P>Q,则x<2015,或x=2015,且y<2014,即可判断出正误;
③设P(x1,y1),Q(x2,y2),M(x3,y3),由P>Q,可得x1>x2或x1=x2,y1>y2.由Q>M,可得x2>x3或x2=x3,y2>y3.分类讨论,即可判断出正误.
④设P(x1,y1),Q(x2,y2),M(x3,y3),则P⊕M=(x1+x3,y1+y3),Q⊕M=(x2+x3,y2+y3);
利用P>Q,可得x1>x2或x1=x2,y1>y2.即可判断出正误.
⑤设P(x1,y1),Q(x2,y2),M(x3,y3),则P?M=x1•x3+y1•y3,Q?M=x2•x3+y2•y3,由P>Q,可得x1>x2或x1=x2,y1>y2,举反例即可判断出正误.
解答 解:①∵P(2015,2014)和Q(2014,2015),2015>2014,则P>Q,正确;
②已知P(2015,2014)和Q(x,y),若P>Q,则x<2015,或x=2015,且y<2014,因此不正确;
③设P(x1,y1),Q(x2,y2),M(x3,y3),∵P>Q,∴x1>x2或x1=x2,y1>y2.∵Q>M,∴x2>x3或x2=x3,y2>y3.当x1>x2,且x2>x3,则x1>x3,∴P>M;
若x1=x2,y1>y2.且x2>x3或x2=x3,y2>y3.同理可得P>M.因此正确.
④设P(x1,y1),Q(x2,y2),M(x3,y3),则P⊕M=(x1+x3,y1+y3),Q⊕M=(x2+x3,y2+y3);
∵P>Q,∴x1>x2或x1=x2,y1>y2.∴x1+x3>x2+x3或x1+x3=x2+x3,y1+y3>y2+y3,∴对任意的点M,都有P⊕M>Q⊕M,正确;
⑤设P(x1,y1),Q(x2,y2),M(x3,y3),则P?M=x1•x3+y1•y3,Q?M=x2•x3+y2•y3,∵P>Q,∴x1>x2或x1=x2,y1>y2,当x1>x2时,取x1=2,x2=-1,x3=-3,y1=1,y2=-2,y3=-3,则P?M=x1•x3+y1•y3=-6-3=-9,Q?M=x2•x3+y2•y3=3+6=9,此时P?M>Q?M不成立;当x1=x2,y1>y2时,取x1=2=x2,x3=-3,y1=1,y2=-2,y3=-3,则P?M=x1•x3+y1•y3=-6-3=-9,Q?M=x2•x3+y2•y3=-6+6=0,此时P?M>Q?M不成立,因此不正确.
故答案为:①③④.
点评 本题考查了新定义“序”及其新运算,考查了分类讨论思想方法、推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
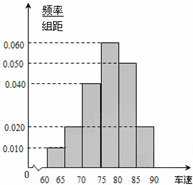 2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.
2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.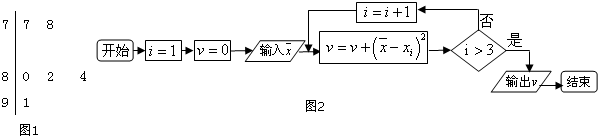 .
.