题目内容
18.已知函数$f(x)=-aln\frac{1}{x}-b{x^2}$图象上一点P(2,f(2))处的切线方程为y=-3x+2ln2+2..(1)求a,b的值;
(2)若方程f(x)+m=0在$[\frac{1}{e},e]$内有两个不等实根,求m的取值范围(其中e为自然对数的底,e≈2.7).
分析 (1)根据函数切线建立方程关系即可求a,b的值;
(2)构造方程,求函数的导数,利用导数进行求解即可.
解答 解(Ⅰ)f′(x)=$\frac{a}{x}$-2bx,f′(2)=$\frac{a}{2}$-4b,f(2)=aln2-4b.
∵点P(2,f(2))处的切线方程为y=-3x+2ln2+2..
∴$\frac{a}{2}$-4b=-3,且aln2-4b=-6+2ln2+2.
解得a=2,b=1.
(Ⅱ)f(x)=2lnx-x2,
令h(x)=f(x)+m=2lnx-x2+m,
则h′(x)=$\frac{2}{x}$-2x=$\frac{2(1-{x}^{2})}{x}$,
令h′(x)=0,得x=1(x=-1舍去).
在$[\frac{1}{e},e]$内,当x∈[$\frac{1}{e}$,1)时,h′(x)>0,∴h(x)是增函数;
当x∈(1,e]时,h′(x)<0,∴h(x)是减函数.
则方程h(x)=0在[$\frac{1}{e}$,e]内有两个不等实根的充要条件是$\left\{\begin{array}{l}{h(\frac{1}{e})≤0}\\{h(1)>0}\\{h(e)≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-2-(\frac{1}{e})^{2}+m≤0}\\{m-1>0}\\{2-{e}^{2}+m≤0}\end{array}\right.$,解得1<m≤2+($\frac{1}{e}$)2.
点评 本题主要考查导数的几何意义以及函数与方程之间的关系,考查学生的运算能力.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
13.甲乙两位同学最近五次模考数学成绩茎叶图如图,则平均分数较高和成绩比较稳定的分别是( )
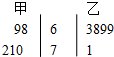
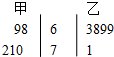
| A. | 甲、甲 | B. | 乙、甲 | C. | 甲、乙 | D. | 乙、乙 |
7.函数f(x)为奇函数且f(3x+1)的周期为3,f(1)=-1,则f(2015)=( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
8.函数y=log${\;}_{\frac{1}{2}}$(sin2xcos$\frac{π}{4}$-cos2xsin$\frac{π}{4}$)的单调递减区间是( )
| A. | (kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$),k∈Z | B. | (kπ+$\frac{π}{8}$,kπ+$\frac{3π}{8}$),k∈Z | ||
| C. | (kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$),k∈Z | D. | (kπ+$\frac{3π}{8}$,kπ+$\frac{5π}{8}$),k∈Z |
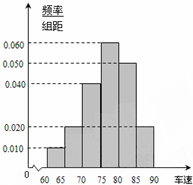 2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.
2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.