题目内容
【题目】已知圆![]() ,圆心为点
,圆心为点![]() ,点
,点![]() 是圆
是圆![]() 内一个定点,
内一个定点,![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() 在圆上运动.
在圆上运动.
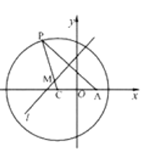
(l)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若![]() 为曲线
为曲线![]() 上任意一点,
上任意一点,![]() |的最大值;
|的最大值;
(3)经过点![]() 且斜率为
且斜率为![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点在
两点在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 坐标:若不存在,说明理由.
坐标:若不存在,说明理由.
【答案】(1) ![]() (2)3;(3) 存在,点
(2)3;(3) 存在,点![]()
【解析】
(1)连接![]() ,根据中垂线性质可知
,根据中垂线性质可知![]() ,可得
,可得![]() ,满足椭圆定义;(2)根据(1)可知,点
,满足椭圆定义;(2)根据(1)可知,点![]() ,
,![]() 是椭圆的焦点,所以
是椭圆的焦点,所以![]() ,利用基本不等式求
,利用基本不等式求![]() 的最大值;(3)假设存在点
的最大值;(3)假设存在点![]() ,设
,设![]() ,直线方程为
,直线方程为![]() ,与椭圆方程联立,得
,与椭圆方程联立,得![]() ,利用韦达定理得到
,利用韦达定理得到![]() ,由
,由![]()
代入坐标表示,求![]() .
.
解:(1)连接![]() ,
,![]() 是线段
是线段![]() 的垂直平分线:
的垂直平分线:
![]()
![]() 点
点![]() 到两定点
到两定点![]() 距离之和为定值
距离之和为定值![]() ,
,
![]() 点
点![]() 的轨迹是以
的轨迹是以![]() 两点为焦点,长轴长为
两点为焦点,长轴长为![]() 的椭圆,
的椭圆,![]()
![]() 动点
动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
(2)![]() 为曲线
为曲线![]() 上任意一点,
上任意一点,![]()
![]() ,当且仅当
,当且仅当![]() 时,等号成立
时,等号成立
(3)假设存在点![]() ,设
,设![]() ,直线方程为
,直线方程为![]() ,代入椭圆方程,得
,代入椭圆方程,得![]()
![]()
![]()
由![]()
![]()
![]()
![]()
由于对任意![]() 恒成立,因此
恒成立,因此![]()
![]() 恒成立
恒成立
即![]() 恒成立
恒成立
![]() 恒成立,因此
恒成立,因此![]()
综上所述,存在点![]() 满足题意
满足题意

 阶梯计算系列答案
阶梯计算系列答案【题目】在中学生综合素质评价某个维度的测评中,分优秀、合格、尚待改进三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表一:男生
男生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 |
| 5 |
表二:女生
女生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 |
|
(1)求![]() ,
,![]() 的值;
的值;
(2)从表一、二中所有尚待改进的学生中随机抽取3人进行交谈,记其中抽取的女生人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(3)由表中统计数据填写![]() 列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 | 45 |
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.01 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |