题目内容
【题目】已知函数![]() .
.
(1)设![]() .
.
①若![]() ,求函数
,求函数![]() 的零点;
的零点;
②若函数![]() 存在零点,求
存在零点,求![]() 的取值范围.
的取值范围.
(2)设![]() ,若对任意
,若对任意![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
【答案】(1)1,![]() ;(2)
;(2)![]() .
.
【解析】
分析:(1)①将![]() 代入解析式,分类讨论解方程即可得结果;②讨论
代入解析式,分类讨论解方程即可得结果;②讨论![]() 的符号,同一坐标系中作出两个函数的图象,利用数形结合可得结果;(2)对任意
的符号,同一坐标系中作出两个函数的图象,利用数形结合可得结果;(2)对任意![]() 恒成立,等价于
恒成立,等价于![]() 的最大值与最小值的差不大于
的最大值与最小值的差不大于![]() ,分三种情况讨论函数的单调性,分别求出最大值与最小值,综合三种情况可得结果.
,分三种情况讨论函数的单调性,分别求出最大值与最小值,综合三种情况可得结果.
详解:(1)F(x)=f(x)﹣g(x)=x﹣a﹣a|x|,
①若a=![]() ,则由F(x)=x﹣
,则由F(x)=x﹣![]() |x|﹣
|x|﹣![]() =0得:
=0得:![]() |x|=x﹣
|x|=x﹣![]() ,
,
当x≥0时,解得:x=1;
当x<0时,解得:x=![]() (舍去);
(舍去);
综上可知,a=![]() 时,函数y=F(x)的零点为1;
时,函数y=F(x)的零点为1;
②若函数y=F(x)存在零点,则x﹣a=a|x|,
当a>0时,作图如下:
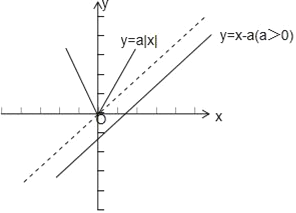
由图可知,当0<a<1时,折线y=a|x|与直线y=x﹣a有交点,即函数y=F(x)存在零点;
同理可得,当﹣1<a<0时,求数y=F(x)存在零点;
又当a=0时,y=x与y=0有交点(0,0),函数y=F(x)存在零点;
综上所述,a的取值范围为(﹣1,1).
(2)∵h(x)=f(x)+g(x)=x﹣a+a|x|,x∈[﹣2,2],
∴当﹣2≤x<0时,h(x)=(1﹣a)x﹣a;
当0≤x≤2时,h(x)=(1+a)x﹣a;
又对任意x1,x2∈[﹣2,2],|h(x1)﹣h(x2)|≤6恒成立,
则h(x1)max﹣h(x2)min≤6,
①当a≤﹣1时,1﹣a>0,1+a≤0,h(x)=(1﹣a)x﹣a在区间[﹣2,0)上单调递增;
h(x)=(1+a)x﹣a在区间[0,2]上单调递减(当a=﹣1时,h(x)=﹣a);
∴h(x)max=h(0)=﹣a,又h(﹣2)=a﹣2,h(2)=2+a,
∴h(x2)min=h(﹣2)=a﹣2,
∴﹣a﹣(a﹣2)=2﹣2a≤6,解得a≥﹣2,
综上,﹣2≤a≤﹣1;
②当﹣1<a<1时,1﹣a>0,1﹣a>0,∴h(x)=(1﹣a)x﹣a在区间[﹣2,0)上单调递增,
且h(x)=(1+a)x﹣a在区间[0,2]上也单调递增,
∴h(x)max=h(2)=2+a,h(x2)min=h(﹣2)=a﹣2,
由a+2﹣(a﹣2)=4≤6恒成立,即﹣1<a<1适合题意;
③当a≥1时,1﹣a≤0,1+a>0,h(x)=(1﹣a)x﹣a在区间[﹣2,0)上单调递减
(当a=1时,h(x)=﹣a),h(x)=(1+a)x﹣a在区间[0,2]上单调递增;
∴h(x)min=h(0)=﹣a;
又h(2)=2+a>a﹣2=h(﹣2),
∴h(x)max=h(2)=2+a,
∴2+a﹣(﹣a)=2+2a≤6,解得a≤2,又a≥1,
∴1≤a≤2;
综上所述,﹣2≤a≤2.