题目内容
【题目】将边长为2的正
沿着高
折起，使
，若折起后
四点都在球
的表面上，则球的表面积为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
通过底面三角形BCD求出底面圆的半径DM，判断球心到底面圆的距离OM，求出球O的半径，即可求解球O的表面积．
△BCD中，BD=1，CD=1，∠BDC=120°，
底面三角形的底面外接圆圆心为M，半径为：r,由余弦定理得到BC=
，再由正弦定理得到
见图示：
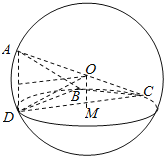
AD是球的弦，DA=，将底面的圆心M平行于AD竖直向上提起，提起到AD的高度的一半，即为球心的位置O，∴OM=
，在直角三角形OMD中，应用勾股定理得到OD，OD即为球的半径.∴球的半径OD=
．
该球的表面积为：4π×OD2=7π；
故选：B．
每日10分钟口算心算速算天天练系列答案
【题目】中国共产党第十九次全国代表大会于2017年10月18日至10月24日在北京召开，会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”，为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚”情况，从某县调查得到农村居民2011年至2017年家庭人均纯收入
（单位：百元）的数据如下表：
注：小康的标准是农村居民家庭年人均纯收入达到8000元.
年 份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入y百元 | 41 | 45 | 48 | 56 | 60 | 64 | 71 |
（Ⅰ）求关于
的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，预测2020年该县农村居民家庭年人均纯收入指标能否达到“全面建成小康社会”的标准？
附：回归直线
斜率和截距的最小二乘估计公式分别为：
，
，其中
.
【题目】某校夏令营有3名男同学
和3名女同学
，其年级情况如下表，现从这6名同学中随机选出2人参加知识竞赛（每人被选到的可能性相同）.
一年级 | 二年级 | 三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
（1）用表中字母列举出所有可能的结果；
（2）设
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件发生的概率．