Question

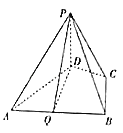
【题目】如图，在四棱锥中，平面，，，，点Q在棱AB上.

（1）证明：平面.

（2）若三棱锥的体积为，求点B到平面PDQ的距离.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）线面垂直只需证明PD和平面内两条相交直线垂直即可，易得，另外中已知三边长通过勾股定理易得,所以平面。（2）点B到平面PDQ的距离通过求得三棱锥的体积和面积即可，而,带入数据求解即可。

（1）证明：在中，，，所以.

所以是直角三角形，且，即.

因为平面PAD，平面PAD，所以.

因为，所以平面ABCD.

（2）解：设.

因为.，所以的面积为.

因为平面ABCD，所以三棱锥的体积为，解得.

因为，所以，所以的面积为.

则三棱锥的体积为.

在中，，，，

则.

设点B到平面PDQ的距离为h，则，解得，

即点B到平面PDQ的距离为.