题目内容
3.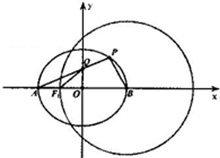 如图,点A,B分别是椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,圆B:(x-2)2+y2=9,经过椭圆E的左焦点F.
如图,点A,B分别是椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,圆B:(x-2)2+y2=9,经过椭圆E的左焦点F.(Ⅰ)求椭圆E的方程;
(Ⅱ)过A作直线l与y轴交于点Q,与椭圆E交于点P(异于A).求$\overrightarrow{{F_1}Q}$•$\overrightarrow{BP}$的取值范围.
分析 (Ⅰ)通过圆B的圆心坐标可得a=2,在圆B方程中令y=0得c=1,进而可得结论;
(Ⅱ)①当直线l为x轴时,显然有$\overrightarrow{{F_1}Q}$•$\overrightarrow{BP}$=0;②设直线AP:x=ty-2,并与椭圆E的方程联立,利用韦达定理可得yP=$\frac{12t}{4+3{t}^{2}}$,xP=$\frac{6{t}^{2}-8}{4+3{t}^{2}}$,通过向量数量积的坐标形式计算即得结论.
解答 解:(Ⅰ)∵以椭圆E的右顶点B为圆心的圆B方程为:(x-2)2+y2=9,
∴圆B的圆心坐标的横坐标即为a的值,∴a=2,
在圆B:(x-2)2+y2=9中令y=0,得F(-1,0),
∴b2=4-1=3,
∴椭圆E的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)①当直线l为x轴时,显然有$\overrightarrow{{F_1}Q}$•$\overrightarrow{BP}$=0;
②设直线AP:x=ty-2,并与椭圆E的方程联立,
消去x可得:(4+3t2)y2-12ty=0,
由椭圆E的方程可知:A(-2,0),
由韦达定理可得:yP=$\frac{12t}{4+3{t}^{2}}$,xP=$\frac{6{t}^{2}-8}{4+3{t}^{2}}$,
在直线AP:x=ty-2中令x=0,得:yQ=$\frac{2}{t}$,
∴$\overrightarrow{{F_1}Q}$•$\overrightarrow{BP}$=(1,$\frac{2}{t}$)•($\frac{6{t}^{2}-8}{4+3{t}^{2}}$-2,$\frac{12t}{4+3{t}^{2}}$)=$\frac{8}{4+3{t}^{2}}$∈(0,2);
综上所述,$\overrightarrow{{F_1}Q}$•$\overrightarrow{BP}$的取值范围为[0,2).
点评 本题考查椭圆的几何性质、直线与椭圆的位置关系、圆与圆的位置关系等基础知识,考查运算求解能力、推理论证能力、探索求解能力,考查数形结合、函数与方程、分类与整合等数学思想,注意解题方法的积累,属于中档题.

| A. | 5 | B. | 8 | C. | 10 | D. | 15 |
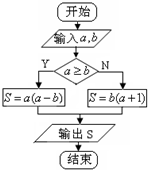
| A. | $\frac{7}{9}$ | B. | $-\frac{8}{3}$ | C. | 4 | D. | -4 |