题目内容
11.求代数式($\root{6}{x}$+$\frac{1}{\root{6}{x}}$)n的展开式.分析 由条件利用二项式定理求得代数式($\root{6}{x}$+$\frac{1}{\root{6}{x}}$)n的展开式.
解答 解:代数式($\root{6}{x}$+$\frac{1}{\root{6}{x}}$)n =${C}_{n}^{0}$•${x}^{\frac{n}{6}}$+${C}_{n}^{1}$•${x}^{\frac{n-1}{6}}$•${x}^{\frac{1}{6}}$+${C}_{n}^{2}$•${x}^{\frac{n-2}{6}}$•${x}^{-\frac{2}{6}}$+…+${C}_{n}^{n}$•${x}^{-\frac{n}{6}}$
${C}_{n}^{0}$•${x}^{\frac{n}{6}}$+${C}_{n}^{1}$•${x}^{\frac{n-2}{6}}$+${C}_{n}^{2}$•${x}^{\frac{n-4}{6}}$+…+${C}_{n}^{n}$•${x}^{-\frac{n}{6}}$.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
3.某次语文考试中考生的分数X~N(80,100),则分数在60-100分的考生占总考生数的百分数为( )
| A. | 68.26% | B. | 95.44% | C. | 99.74% | D. | 31.74% |
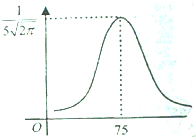 某市高二理科学生数学考试的成绩x服从正态分布,其密度函数为f(x)=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}$,密度曲线如图,已知该市理科学生总数是10000人,则成绩位于(65,85]的人数约是9544.
某市高二理科学生数学考试的成绩x服从正态分布,其密度函数为f(x)=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}$,密度曲线如图,已知该市理科学生总数是10000人,则成绩位于(65,85]的人数约是9544.