Question

19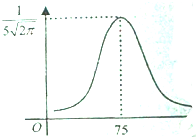．某市高二理科学生数学考试的成绩x服从正态分布，其密度函数为f（x）=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{（x-μ）^{2}}{2{σ}^{2}}}$，密度曲线如图，已知该市理科学生总数是10000人，则成绩位于（65，85]的人数约是9544．

Answer 1

分析 由题图知 X～N（μ，σ²），其中μ=75，σ=5，P（μ-2σ＜X≤μ+2σ）=P（65＜X≤85）=0.9544，从而得出成绩在（65，85]范围内的学生人数．

解答 解：由题图知 X～N（μ，σ²），其中μ=75，σ=5，
∴P（μ-2σ＜X≤μ+2σ）=P（65＜X≤85）=0.9544．
∴人数为0.9544×10000=9544．
故答案为：9544．

点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查曲线的变化特点，本题是一个基础题．