题目内容
2.已知直线l:x=-2,l与x轴交于点A,动点M(x,y)到直线l的距离比到点N(1,0)的距离大1.(1)求点M的轨迹W的方程;
(2)过点A作斜率为k的直线交曲线W于B,C两点,设$\overrightarrow{AB}$=λ$\overrightarrow{AC}$,若$\frac{1}{7}$≤λ≤1,求k的取值范围.
分析 (1)利用抛物线定义“到定点距离等于到定直线距离的点的轨迹”求动点P的轨迹;
(2)直线l方程为y=kx+2,代入曲线方程,利用韦达定理及向量知识,可求直线斜率k的取值范围.
解答 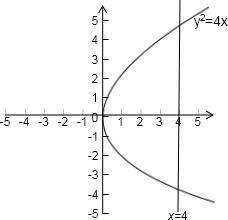 解:(1)因为动点M到直线x=-2的距离比它到点N(1,0)的距离大1,
解:(1)因为动点M到直线x=-2的距离比它到点N(1,0)的距离大1,
所以动点M到直线x=-1的距离与它到点F(1,0)的距离相等,
故所求轨迹为:以原点为顶点,开口向右的抛物线y2=4x.
(2)设B(x1,y1),C(x2,y2),
则y${\;}_{1}^{2}$=4x1,${y}_{2}^{2}$=4x2,
∴$\overrightarrow{AB}$=(x1+2,y1),$\overrightarrow{BC}$=(x2-x1,y2-y1),
由$\overrightarrow{AB}=2\overrightarrow{BC}$可得:y1=2(y2-y1),即$\frac{{y}_{2}}{{y}_{1}}$=$\frac{3}{2}$,
∴$\frac{{x}_{2}}{{x}_{1}}$=$\frac{9}{4}$…①
设直线AB的方程为y=k(x+2),(k≠0),可得$\left\{\begin{array}{l}{y=k(x+2)}\\{{y}^{2}=4x}\end{array}\right.$消去y,得:k2x2+4(k2-1)x+4k2=0,
由根与系数的关系可得:x1+x2=$\frac{4-4{k}^{2}}{{k}^{2}}$…②
x1x2=4…③
由①③,得x1=$\frac{4}{3}$,x2=3,代入②,得k2=$\frac{12}{25}$,
所以k=±$\frac{2\sqrt{3}}{5}$.
点评 本题考查轨迹方程,考查向量知识的运用,考查直线与曲线的位置关系,考查韦达定理的运用,属于基本知识的考查.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 8 | B. | 12 | C. | $\frac{2}{9}$ | D. | 16 |