题目内容
(本小题满分14分)规定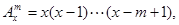 其中x∈R,m为正整数,且
其中x∈R,m为正整数,且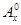 =1,这是排列数A
=1,这是排列数A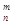 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.
(1)求A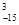 的值; (2)确定函数
的值; (2)确定函数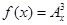 的单调区间.
的单调区间.
(3) 若关于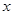 的方程
的方程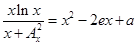 只有一个实数根, 求
只有一个实数根, 求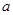 的值.
的值.
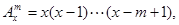 其中x∈R,m为正整数,且
其中x∈R,m为正整数,且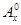 =1,这是排列数A
=1,这是排列数A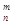 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.(1)求A
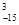 的值; (2)确定函数
的值; (2)确定函数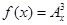 的单调区间.
的单调区间.(3) 若关于
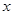 的方程
的方程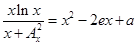 只有一个实数根, 求
只有一个实数根, 求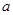 的值.
的值.(1)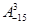 =(-15)(-16)(-17)=4080;
=(-15)(-16)(-17)=4080;
(2)增区间为(-∞,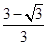 ),(
),(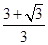 ,+∞);减区间为[
,+∞);减区间为[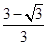 ,
,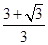 ];
];
(3)当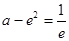 , 即
, 即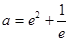 时, 方程
时, 方程 只有一个根.
只有一个根.
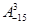 =(-15)(-16)(-17)=4080;
=(-15)(-16)(-17)=4080; (2)增区间为(-∞,
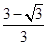 ),(
),(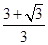 ,+∞);减区间为[
,+∞);减区间为[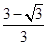 ,
,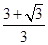 ];
];(3)当
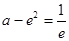 , 即
, 即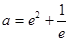 时, 方程
时, 方程 只有一个根.
只有一个根. (1)根据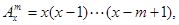 可求出
可求出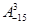 =(-15)(-16)(-17)=4080.
=(-15)(-16)(-17)=4080.
(2)先求导数,得(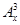 )/=3x2-6x+2.根据导数大于零,求单调增区间.导数小于零,求单调减区间.
)/=3x2-6x+2.根据导数大于零,求单调增区间.导数小于零,求单调减区间.
(3)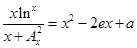 , 得
, 得
令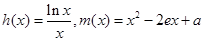 ,然后利用导数确定h(x)的图像,作出m(x)的图像,根据图像可确定它们有一个公共点时,a的取值范围.
,然后利用导数确定h(x)的图像,作出m(x)的图像,根据图像可确定它们有一个公共点时,a的取值范围.
解:(1)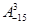 =(-15)(-16)(-17)=4080;………3分
=(-15)(-16)(-17)=4080;………3分
(2)先求导数,得(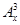 )/=3x2-6x+2.令3x2-6x+2>0,解得x<
)/=3x2-6x+2.令3x2-6x+2>0,解得x<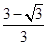 或x>
或x>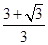
因此,当x∈(-∞,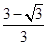 )时,函数为增函数,当x∈(
)时,函数为增函数,当x∈(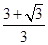 ,+∞)时,函数也为增函数.
,+∞)时,函数也为增函数.
令3x2-6x+2≤0, 解得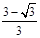 ≤x≤
≤x≤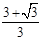 ,因此,当x∈[
,因此,当x∈[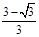 ,
,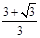 ]时,函数为减函数.
]时,函数为减函数.
∴函数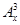 的增区间为(-∞,
的增区间为(-∞,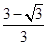 ),(
),(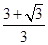 ,+∞);减区间为[
,+∞);减区间为[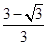 ,
,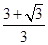 ]……7分
]……7分
(3) 解: 由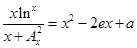 , 得
, 得 .
.
令 , 则
, 则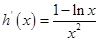 .………8分
.………8分
令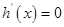 , 得
, 得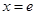 .
.
当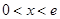 时,
时, 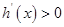 ; 当
; 当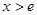 时,
时, 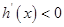 .
.
∴函数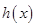 在区间
在区间 上单调递增, 在区间
上单调递增, 在区间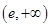 上单调递减.
上单调递减.
∴当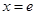 时, 函数
时, 函数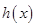 取得最大值, 其值为
取得最大值, 其值为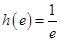 . …… 10分
. …… 10分
而函数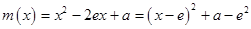 ,
,
当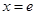 时, 函数
时, 函数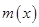 取得最小值, 其值为
取得最小值, 其值为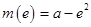 . …… 12分
. …… 12分
∴ 当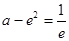 , 即
, 即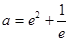 时, 方程
时, 方程 只有一个根. …… 14分
只有一个根. …… 14分
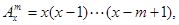 可求出
可求出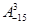 =(-15)(-16)(-17)=4080.
=(-15)(-16)(-17)=4080.(2)先求导数,得(
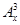 )/=3x2-6x+2.根据导数大于零,求单调增区间.导数小于零,求单调减区间.
)/=3x2-6x+2.根据导数大于零,求单调增区间.导数小于零,求单调减区间.(3)
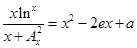 , 得
, 得
令
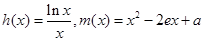 ,然后利用导数确定h(x)的图像,作出m(x)的图像,根据图像可确定它们有一个公共点时,a的取值范围.
,然后利用导数确定h(x)的图像,作出m(x)的图像,根据图像可确定它们有一个公共点时,a的取值范围.解:(1)
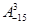 =(-15)(-16)(-17)=4080;………3分
=(-15)(-16)(-17)=4080;………3分(2)先求导数,得(
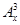 )/=3x2-6x+2.令3x2-6x+2>0,解得x<
)/=3x2-6x+2.令3x2-6x+2>0,解得x<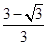 或x>
或x>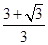
因此,当x∈(-∞,
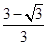 )时,函数为增函数,当x∈(
)时,函数为增函数,当x∈(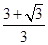 ,+∞)时,函数也为增函数.
,+∞)时,函数也为增函数.令3x2-6x+2≤0, 解得
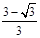 ≤x≤
≤x≤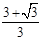 ,因此,当x∈[
,因此,当x∈[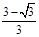 ,
,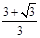 ]时,函数为减函数.
]时,函数为减函数. ∴函数
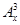 的增区间为(-∞,
的增区间为(-∞,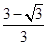 ),(
),(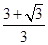 ,+∞);减区间为[
,+∞);减区间为[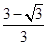 ,
,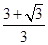 ]……7分
]……7分(3) 解: 由
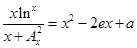 , 得
, 得 .
.令
 , 则
, 则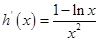 .………8分
.………8分令
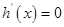 , 得
, 得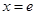 .
.当
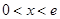 时,
时, 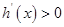 ; 当
; 当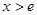 时,
时, 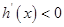 .
.∴函数
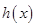 在区间
在区间 上单调递增, 在区间
上单调递增, 在区间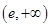 上单调递减.
上单调递减.∴当
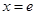 时, 函数
时, 函数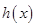 取得最大值, 其值为
取得最大值, 其值为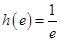 . …… 10分
. …… 10分而函数
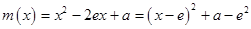 ,
,当
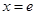 时, 函数
时, 函数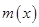 取得最小值, 其值为
取得最小值, 其值为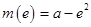 . …… 12分
. …… 12分∴ 当
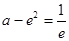 , 即
, 即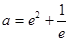 时, 方程
时, 方程 只有一个根. …… 14分
只有一个根. …… 14分
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,对给定的正整数
,对给定的正整数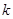 ,若在其定义域内存在实数
,若在其定义域内存在实数 ,使得
,使得 ,则称函数
,则称函数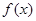 为“
为“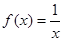 是否为“
是否为“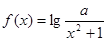 为“2性质函数”,求实数
为“2性质函数”,求实数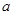 的取值范围;
的取值范围;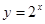 与
与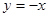 的图像有公共点,求证:
的图像有公共点,求证: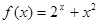 为“1性质函数”。
为“1性质函数”。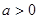 ,函数
,函数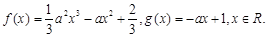
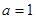 时,求函数
时,求函数 在点(1,
在点(1,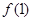 )的切线方程;
)的切线方程;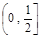 上至少存在一个实数x0,使
上至少存在一个实数x0,使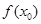 >g(xo)成立,求正实数
>g(xo)成立,求正实数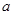 的取值范围。
的取值范围。 其中
其中 为自然对数的底数,
为自然对数的底数,  .(Ⅰ)设
.(Ⅰ)设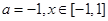 ,求函数
,求函数 的最值;(Ⅱ)若对于任意的
的最值;(Ⅱ)若对于任意的 ,都有
,都有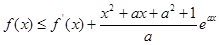 成立,求
成立,求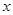 的取值范围.
的取值范围.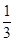 x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )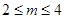
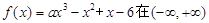 上既有极大值又有极小值,则
上既有极大值又有极小值,则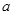 的取值范围为
的取值范围为



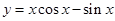 在下面哪个区间是增函数 ( )
在下面哪个区间是增函数 ( )



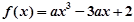 的图象经过四个象限,则实数
的图象经过四个象限,则实数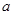 的取值范围是( )
的取值范围是( )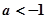 ,或
,或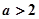

 ,或
,或