题目内容
已知函数 其中
其中 为自然对数的底数,
为自然对数的底数,  .(Ⅰ)设
.(Ⅰ)设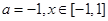 ,求函数
,求函数 的最值;(Ⅱ)若对于任意的
的最值;(Ⅱ)若对于任意的 ,都有
,都有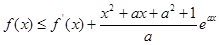 成立,求
成立,求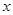 的取值范围.
的取值范围.
 其中
其中 为自然对数的底数,
为自然对数的底数,  .(Ⅰ)设
.(Ⅰ)设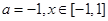 ,求函数
,求函数 的最值;(Ⅱ)若对于任意的
的最值;(Ⅱ)若对于任意的 ,都有
,都有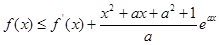 成立,求
成立,求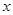 的取值范围.
的取值范围.(Ⅰ)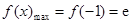 ,
,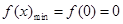 . (Ⅱ)
. (Ⅱ)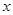 的取值范围是
的取值范围是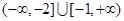
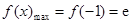 ,
,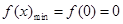 . (Ⅱ)
. (Ⅱ)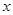 的取值范围是
的取值范围是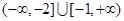
第一问中,当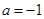 时,
时,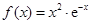 ,
, .结合表格和导数的知识判定单调性和极值,进而得到最值。
.结合表格和导数的知识判定单调性和极值,进而得到最值。
第二问中,∵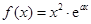 ,
,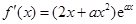 ,
,
∴原不等式等价于: ,
,
即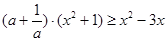 , 亦即
, 亦即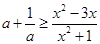
分离参数的思想求解参数的范围
解:(Ⅰ)当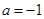 时,
时,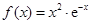 ,
, .
.
当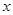 在
在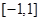 上变化时,
上变化时,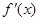 ,
,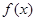 的变化情况如下表:
的变化情况如下表:
∴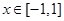 时,
时,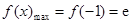 ,
,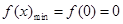 .
.
(Ⅱ)∵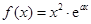 ,
,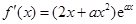 ,
,
∴原不等式等价于: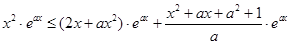 ,
,
即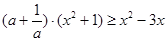 , 亦即
, 亦即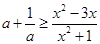 .
.
∴对于任意的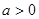 ,原不等式恒成立,等价于
,原不等式恒成立,等价于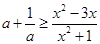 对
对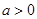 恒成立,
恒成立,
∵对于任意的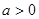 时,
时, 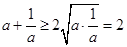 (当且仅当
(当且仅当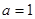 时取等号).
时取等号).
∴只需 ,即
,即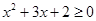 ,解之得
,解之得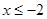 或
或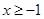 .
.
因此,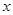 的取值范围是
的取值范围是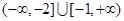
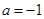 时,
时,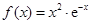 ,
, .结合表格和导数的知识判定单调性和极值,进而得到最值。
.结合表格和导数的知识判定单调性和极值,进而得到最值。第二问中,∵
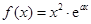 ,
,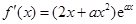 ,
, ∴原不等式等价于:
 ,
,即
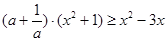 , 亦即
, 亦即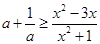
分离参数的思想求解参数的范围
解:(Ⅰ)当
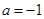 时,
时,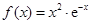 ,
, .
. 当
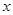 在
在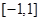 上变化时,
上变化时,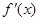 ,
,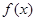 的变化情况如下表:
的变化情况如下表: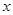 | 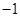 | 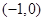 |  | 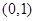 | 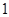 |
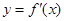 | | - |  | + | |
 | 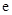 |  |  |  | 1/e |
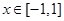 时,
时,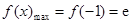 ,
,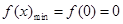 .
. (Ⅱ)∵
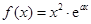 ,
,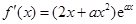 ,
, ∴原不等式等价于:
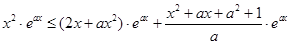 ,
,即
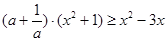 , 亦即
, 亦即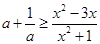 .
.∴对于任意的
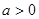 ,原不等式恒成立,等价于
,原不等式恒成立,等价于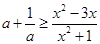 对
对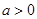 恒成立,
恒成立, ∵对于任意的
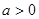 时,
时, 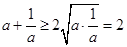 (当且仅当
(当且仅当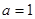 时取等号).
时取等号).∴只需
 ,即
,即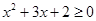 ,解之得
,解之得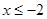 或
或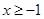 .
.因此,
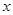 的取值范围是
的取值范围是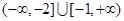

练习册系列答案
相关题目

 =
= 时,求曲线
时,求曲线 在点(
在点( ,
, )处的切线方程。
)处的切线方程。 若不存在,说明理由。若存在,求出
若不存在,说明理由。若存在,求出 ,函数
,函数 .
. 时,
时, ,求函数
,求函数 的单调区间;
的单调区间; 的不等式
的不等式 在区间
在区间 上有解,求
上有解,求 的取值范围;
的取值范围; 在其图象上的两点
在其图象上的两点 ,
, (
(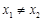 )处的切线分别为
)处的切线分别为 .若直线
.若直线 与
与 平行,试探究点
平行,试探究点 与点
与点 的关系,并证明你的结论.
的关系,并证明你的结论.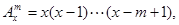 其中x∈R,m为正整数,且
其中x∈R,m为正整数,且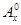 =1,这是排列数A
=1,这是排列数A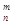 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.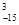 的值; (2)确定函数
的值; (2)确定函数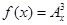 的单调区间.
的单调区间.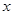 的方程
的方程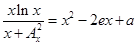 只有一个实数根, 求
只有一个实数根, 求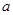 的值.
的值.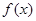
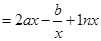 .
.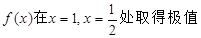 ,
, 的值;
的值;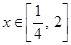 存在
存在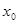 ,使得不等式
,使得不等式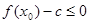 成立,求c最小值。(参考数据
成立,求c最小值。(参考数据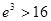 )
)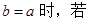
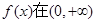 上是单调函数,求
上是单调函数,求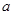 的取值范围。
的取值范围。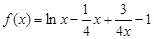 .
.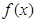 的单调区间;
的单调区间;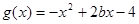 ,若对任意
,若对任意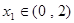 ,
,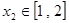 ,不等式
,不等式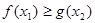 恒成立,求实数
恒成立,求实数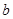 的取值范围.
的取值范围.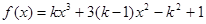 在区间(0,4)上是减函数,则
在区间(0,4)上是减函数,则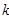 的取值范围是 ( )
的取值范围是 ( ) 



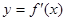 的图象可能为( )
的图象可能为( )