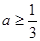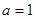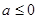题目内容
(本小题满分12分)已知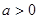 ,函数
,函数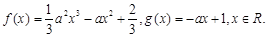
(1)当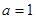 时,求函数
时,求函数 在点(1,
在点(1,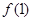 )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在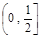 上至少存在一个实数x0,使
上至少存在一个实数x0,使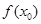 >g(xo)成立,求正实数
>g(xo)成立,求正实数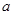 的取值范围。
的取值范围。
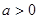 ,函数
,函数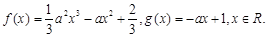
(1)当
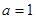 时,求函数
时,求函数 在点(1,
在点(1,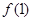 )的切线方程;
)的切线方程;(2)求函数
 在[-1,1]的极值;
在[-1,1]的极值;(3)若在
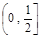 上至少存在一个实数x0,使
上至少存在一个实数x0,使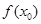 >g(xo)成立,求正实数
>g(xo)成立,求正实数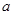 的取值范围。
的取值范围。(Ⅰ) 函数 在点(1,
在点(1,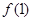 )的切线方程为
)的切线方程为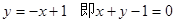 ;
;
(Ⅱ)当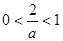 即
即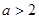 时,
时, 的极大值是
的极大值是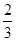 ,极小值是
,极小值是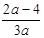
① 当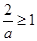 即
即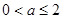 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为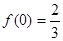 ,无极小值。
,无极小值。
综上所述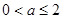 时,极大值为
时,极大值为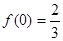 ,无极小值
,无极小值
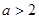 时 极大值是
时 极大值是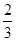 ,极小值是
,极小值是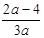
(Ⅲ)(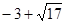
 ,
,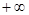 ) .
) .
 在点(1,
在点(1,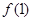 )的切线方程为
)的切线方程为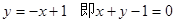 ;
;(Ⅱ)当
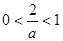 即
即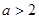 时,
时, 的极大值是
的极大值是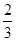 ,极小值是
,极小值是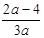
① 当
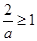 即
即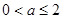 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为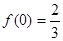 ,无极小值。
,无极小值。 综上所述
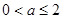 时,极大值为
时,极大值为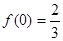 ,无极小值
,无极小值 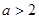 时 极大值是
时 极大值是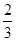 ,极小值是
,极小值是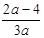
(Ⅲ)(
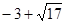
 ,
,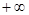 ) .
) .本试题主要考查了导数在研究函数中的运用。 利用导数的几何意义求解切线方程,并结合导数的符号与单调性的关系,求解函数的极值,并分析方程根的问题的综合运用。
(1)先求解函数定义域和导数,然后得到切点处的导数值即为切线的斜率,利用点斜式得到方程。
(2)因为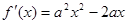 是关于含有参数的二次函数形式,那么对于参数a分情况讨论得到单调性和极值问题。
是关于含有参数的二次函数形式,那么对于参数a分情况讨论得到单调性和极值问题。
(3)构造新的函数设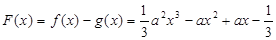 ,
,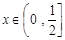 ,利用导数的思想求解其最大值即可。便可以得到a的范围。
,利用导数的思想求解其最大值即可。便可以得到a的范围。
解:(Ⅰ)∵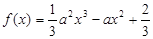 ∴
∴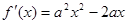
∴ 当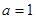 时,
时,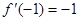 又
又 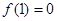
∴ 函数 在点(1,
在点(1,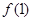 )的切线方程为
)的切线方程为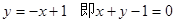 --------4分
--------4分
(Ⅱ)令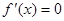 有
有 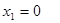
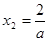
② 当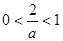 即
即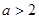 时
时
故 的极大值是
的极大值是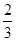 ,极小值是
,极小值是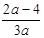
③ 当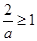 即
即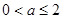 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为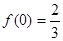 ,无极小值。
,无极小值。
综上所述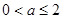 时,极大值为
时,极大值为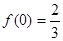 ,无极小值
,无极小值
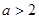 时 极大值是
时 极大值是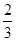 ,极小值是
,极小值是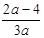 ----------8分
----------8分
(Ⅲ)设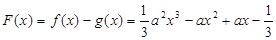 ,
,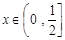
对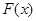 求导,得
求导,得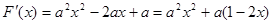
∵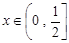 ,
,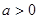
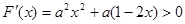
∴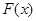 在区间
在区间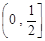 上为增函数,则
上为增函数,则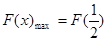
依题意,只需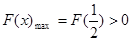 ,即
,即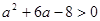
解得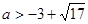 或
或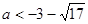 (舍去)
(舍去)
则正实数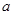 的取值范围是(
的取值范围是(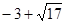
 ,
,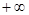 ) ----------12分
) ----------12分
(1)先求解函数定义域和导数,然后得到切点处的导数值即为切线的斜率,利用点斜式得到方程。
(2)因为
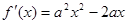 是关于含有参数的二次函数形式,那么对于参数a分情况讨论得到单调性和极值问题。
是关于含有参数的二次函数形式,那么对于参数a分情况讨论得到单调性和极值问题。(3)构造新的函数设
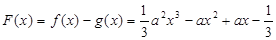 ,
,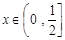 ,利用导数的思想求解其最大值即可。便可以得到a的范围。
,利用导数的思想求解其最大值即可。便可以得到a的范围。解:(Ⅰ)∵
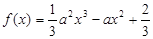 ∴
∴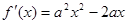
∴ 当
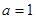 时,
时,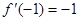 又
又 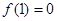
∴ 函数
 在点(1,
在点(1,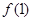 )的切线方程为
)的切线方程为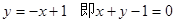 --------4分
--------4分(Ⅱ)令
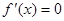 有
有 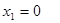
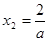
② 当
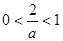 即
即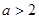 时
时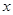 | (-1,0) | 0 | (0,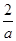 ) ) | 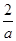 | (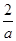 ,1) ,1) |
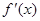 | + | 0 | - | 0 | + |
 |   | 极大值 |   | 极小值 |   |
 的极大值是
的极大值是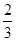 ,极小值是
,极小值是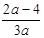
③ 当
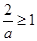 即
即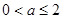 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为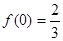 ,无极小值。
,无极小值。 综上所述
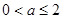 时,极大值为
时,极大值为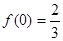 ,无极小值
,无极小值 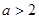 时 极大值是
时 极大值是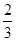 ,极小值是
,极小值是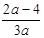 ----------8分
----------8分(Ⅲ)设
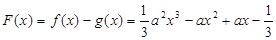 ,
,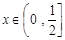
对
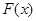 求导,得
求导,得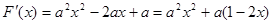
∵
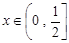 ,
,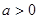
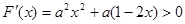
∴
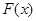 在区间
在区间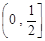 上为增函数,则
上为增函数,则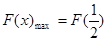
依题意,只需
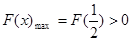 ,即
,即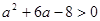
解得
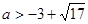 或
或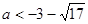 (舍去)
(舍去)则正实数
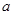 的取值范围是(
的取值范围是(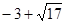
 ,
,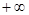 ) ----------12分
) ----------12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
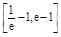 时,不等式f(x)<m恒成立,求实数m的值;
时,不等式f(x)<m恒成立,求实数m的值;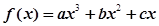 在
在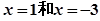 处取得极值,且
处取得极值,且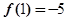
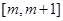 上单调递增,求
上单调递增,求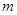 的取值范围
的取值范围
 =
= 时,求曲线
时,求曲线 在点(
在点( ,
, )处的切线方程。
)处的切线方程。 若不存在,说明理由。若存在,求出
若不存在,说明理由。若存在,求出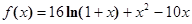 .
.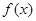 的单调区间;
的单调区间;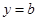 与函数
与函数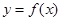 的图像有
的图像有 个交点,求
个交点,求 的取值范围.
的取值范围. .
. 时,求函数
时,求函数 的单调区间;
的单调区间; ,使得函数
,使得函数 ?若存在,,求
?若存在,,求 ,总有
,总有 ,则称
,则称 是
是 的凸
的凸 ,则称
,则称 时,利用定义分析
时,利用定义分析 。
。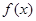 有最大值
有最大值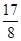 ,求实数
,求实数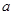 的值;
的值;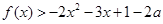 对一切实数
对一切实数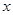 恒成立,求实数
恒成立,求实数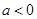 ,解不等式
,解不等式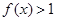 。
。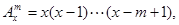 其中x∈R,m为正整数,且
其中x∈R,m为正整数,且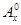 =1,这是排列数A
=1,这是排列数A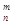 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.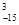 的值; (2)确定函数
的值; (2)确定函数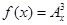 的单调区间.
的单调区间.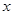 的方程
的方程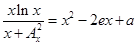 只有一个实数根, 求
只有一个实数根, 求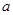 的值.
的值.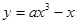 在R上时减函数,则
在R上时减函数,则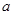 的取值范围为:( )
的取值范围为:( )