题目内容
14.在正三棱柱A1B1C1-ABC中,AB=AA1=1,边AB上有一点P,锐二面角P-A1C1-B1与P-B1C1-A1的大小分别为α、β,则tan(α+β)的最小值为-$\frac{8\sqrt{3}}{13}$.分析 设AP=x,则PB=1-x,先利用条件以及正三棱柱的性质,二面角的平面角的定义求出tanα和tanβ的值,再利用两角和的正切公式求得tan(α+β)的解析式,从而求得它的最小值.
解答 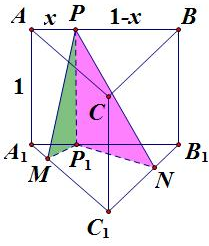 解:如图所示:作PP1⊥A1B1,P1 为垂足; P1M⊥A1C1,M为垂足,P1N⊥B1C1,N为垂足,
解:如图所示:作PP1⊥A1B1,P1 为垂足; P1M⊥A1C1,M为垂足,P1N⊥B1C1,N为垂足,
则由题意可得α=∠PMP1,β=∠PNP1.
设AP=x,则PB=1-x,MP1=$\frac{\sqrt{3}}{2}$x,NP1=$\frac{\sqrt{3}}{2}$(1-x),
故tanα=$\frac{{PP}_{1}}{{MP}_{1}}$=$\frac{1}{\frac{\sqrt{3}x}{2}}$=$\frac{2}{x\sqrt{3}}$ tanβ=$\frac{{PP}_{1}}{{NP}_{1}}$=$\frac{1}{\frac{\sqrt{3}(1-x)}{2}}$=$\frac{2}{\sqrt{3}(1-x)}$,
故tan(α+β)=$\frac{tanα+tanβ}{1-tanα•tanβ}$=$\frac{\frac{2}{x\sqrt{3}}+\frac{2}{\sqrt{3}(1-x)}}{1-\frac{2}{x\sqrt{3}}•\frac{2}{\sqrt{3}(1-x)}}$=$\frac{2\sqrt{3}}{3x(1-x)-4}$,
故当x=$\frac{1}{2}$时,3x(1-x)-4取得最大值为-$\frac{13}{4}$,tan(α+β)=$\frac{2\sqrt{3}}{3x(1-x)-4}$ 取得最小值为-$\frac{8\sqrt{3}}{13}$.
点评 本题主要考查正三棱柱的性质,二面角的平面角的定义及求法,两角和的正切公式的应用,属于中档题.

 名校课堂系列答案
名校课堂系列答案
| A. | ($\frac{\sqrt{3}}{4}$-$\frac{1}{4}$,$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$) | B. | ($\frac{\sqrt{3}}{2}$-$\frac{1}{2}$,$\frac{1}{2}$-$\frac{\sqrt{3}}{4}$) | C. | ($\frac{\sqrt{3}}{2}$-$\frac{1}{4}$,$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$) | D. | ($\frac{\sqrt{3}}{2}$-$\frac{1}{4}$,$\frac{\sqrt{3}}{4}$-$\frac{1}{2}$) |
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | 在圆外 | B. | 在圆上 | C. | 在圆内 | D. | 无法确定 |
| A. | a6>b6或a6<b6 | B. | a6<b6 | C. | a6>b6 | D. | a6=b6 |