题目内容
5．已知函数f（x）=$\frac{sin2x-cos2x+1}{2sinx}$．（1）求函数f（x）的定义域；
（2）求函数f（x）的值域．
分析 （1）根据解析式得出）sinx≠0，求解即可．
（2）把解析式化简得出f（x）=$\sqrt{2}$sin（x+$\frac{π}{4}$），根据三角函数的有界性得出值域即可．
解答 解：∵函数f（x）=$\frac{sin2x-cos2x+1}{2sinx}$．
∴（1）sinx≠0，x≠kπ，k∈Z，
∴函数f（x）的定义域：{x|x≠kπ，k∈Z}，
（2）函数f（x）=$\frac{sin2x-cos2x+1}{2sinx}$=$\sqrt{2}$sin（x+$\frac{π}{4}$），
∵-1≤sin（x+$\frac{π}{4}$）≤1，
∴$-\sqrt{2}≤$$\sqrt{2}$sin（x+$\frac{π}{4}$）$≤\sqrt{2}$，
∴函数f（x）的值域：[-$\sqrt{2}，\sqrt{2}$]
点评 本题考查了函数定义，性质，三角函数的性质，难度不大，属于简单的综合试题．
练习册系列答案
相关题目
16．定义运算：$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3，已知函数f（x）=$|\begin{array}{l}{sinx}&{-1}\\{1}&{cosx}\end{array}|$，则函数f（x）的最小正周期是（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | 2π | D． | 4π |
17．定义：如果函数f（x）在[a，b]上存在x1，x2 （a＜x1＜x2＜b），满足f′（x1）=$\frac{f（b）-f（a）}{b-a}$，f′（x2）=$\frac{f′（b）-f′（a）}{b-a}$，则称数x1，x2 为[a，b]上的“对望数”函数f（x）为[a，b]上的“对望函数”，已知函数f（x）=$\frac{1}{3}{x}^{3}-{x}^{2}+m$是[0，m]上的“对望函数”，则实数m的取值范围是（ ）
| A． | （1，$\frac{3}{2}$） | B． | （1，$\frac{3}{2}$）∪（$\frac{3}{2}$，3） | C． | （2，3） | D． | （$\frac{3}{2}$，3） |
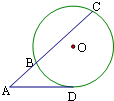如图，从圆O外一点A引圆的切线AD和割线ABC，已知AD=2$\sqrt{3}$，BC=2AB，圆心O到AC的距离为$\sqrt{5}$，则点A与圆O上的点的最短距离为$\sqrt{21}-3$．