Question

【题目】在四棱锥中，平面ABCD，是正三角形，AC与BD的交点为M，又，，点N是CD中点．

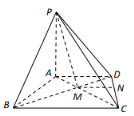
（1）求证：平面PAD；

（2）求点M到平面PBC的距离．

Answer 1

【答案】(1)证明见解析；(2)

【解析】

（1）推导出△ABD≌△BCD，从而MN∥AD，由此能证明MN∥平面PAD．
（2）设M到平面PBC的距离为h，由VM-PBC=VP-BMC，能求出点M到平面PBC的距离．

（1）是正三角形，所以，又，

∴BD所在直线为线段AC的垂直平分线，

所以M为AC的中点，

又点N是CD中点，所以，

又平面PAD，平面PAD，

所以平面PAD；

（2）解：设M到平面PBC的距离为h，在中，，

所以

在中，，所以，

在中，，，，所以.

由．即，

解得．

所以点M到平面PBC的距离为