题目内容
定义:已知函数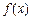 在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数
在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数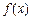 在[m,n] (m<n)上具有“DK”性质.
在[m,n] (m<n)上具有“DK”性质.
(1)判断函数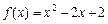 在[1,2]上是否具有“DK”性质,说明理由;
在[1,2]上是否具有“DK”性质,说明理由;
(2)若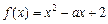 在[a,a+1]上具有“DK”性质,求a的取值范围.
在[a,a+1]上具有“DK”性质,求a的取值范围.
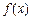 在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数
在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数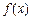 在[m,n] (m<n)上具有“DK”性质.
在[m,n] (m<n)上具有“DK”性质.(1)判断函数
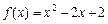 在[1,2]上是否具有“DK”性质,说明理由;
在[1,2]上是否具有“DK”性质,说明理由;(2)若
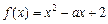 在[a,a+1]上具有“DK”性质,求a的取值范围.
在[a,a+1]上具有“DK”性质,求a的取值范围.解:(1)∵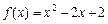 ,x∈[1,2],
,x∈[1,2],
∴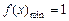 ≤1,
≤1,
∴函数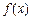 在[1,2]上具有“DK”性质……………………………………6分
在[1,2]上具有“DK”性质……………………………………6分
(2)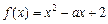 ,x∈[a,a+1],其对称轴为
,x∈[a,a+1],其对称轴为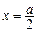 .
.
①当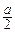 ≤a时,即a≥0时,函
≤a时,即a≥0时,函 数
数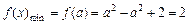 .
.
若函数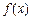 具有“DK”性质,则有2≤a总成立,即a≥2.…………8分
具有“DK”性质,则有2≤a总成立,即a≥2.…………8分
②当a<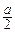 <a+1,即-2<a<0时,
<a+1,即-2<a<0时,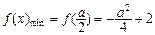 .
.
若函数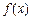 具有“DK”性质,则有
具有“DK”性质,则有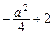 ≤a总成立,
≤a总成立,
解得a∈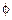 .…………………………………………………………………10分
.…………………………………………………………………10分
③当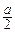 ≥a+1,即a≤-2时,函数
≥a+1,即a≤-2时,函数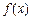 的最小值为
的最小值为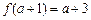 .
.
若函数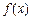 具有“DK”性质,
具有“DK”性质, 则有a+3≤a,解得a∈
则有a+3≤a,解得a∈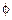 .………… 12分
.………… 12分
综上所述,若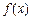 在[a,a+1]上具有“DK”性质,则a≥2.………… 14分
在[a,a+1]上具有“DK”性质,则a≥2.………… 14分
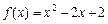 ,x∈[1,2],
,x∈[1,2],∴
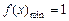 ≤1,
≤1,∴函数
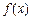 在[1,2]上具有“DK”性质……………………………………6分
在[1,2]上具有“DK”性质……………………………………6分(2)
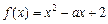 ,x∈[a,a+1],其对称轴为
,x∈[a,a+1],其对称轴为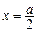 .
.①当
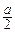 ≤a时,即a≥0时,函
≤a时,即a≥0时,函 数
数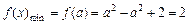 .
.若函数
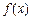 具有“DK”性质,则有2≤a总成立,即a≥2.…………8分
具有“DK”性质,则有2≤a总成立,即a≥2.…………8分②当a<
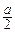 <a+1,即-2<a<0时,
<a+1,即-2<a<0时,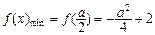 .
.若函数
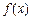 具有“DK”性质,则有
具有“DK”性质,则有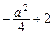 ≤a总成立,
≤a总成立,解得a∈
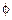 .…………………………………………………………………10分
.…………………………………………………………………10分③当
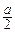 ≥a+1,即a≤-2时,函数
≥a+1,即a≤-2时,函数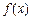 的最小值为
的最小值为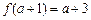 .
.若函数
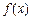 具有“DK”性质,
具有“DK”性质, 则有a+3≤a,解得a∈
则有a+3≤a,解得a∈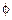 .………… 12分
.………… 12分综上所述,若
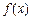 在[a,a+1]上具有“DK”性质,则a≥2.………… 14分
在[a,a+1]上具有“DK”性质,则a≥2.………… 14分 略

练习册系列答案
相关题目
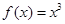 (
(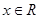 ),则函数
),则函数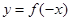 在其定义域上是
在其定义域上是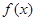 在区间
在区间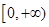 单调递增,
单调递增,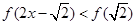 的
的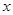 取值
取值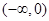
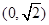
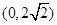
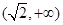
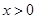 ,函数
,函数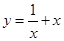 的最小值是 ( )
的最小值是 ( )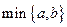 表示
表示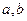 两数中的最小值,若函数
两数中的最小值,若函数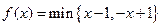 ,则不等式
,则不等式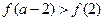 的解集是 .
的解集是 .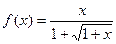
 ,
,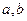 为两个不相等的正实数,则下列不等式正确
为两个不相等的正实数,则下列不等式正确 的是( )
的是( )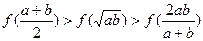 B.
B.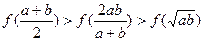 C.
C.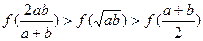 D.
D.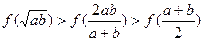
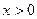 ,则函数
,则函数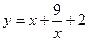 有( )
有( ) 值11
值11