题目内容
已知偶函数
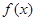 在区间
在区间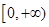 单调递增,
单调递增,则满足
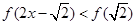 的
的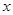 取值
取值范围是( )
A.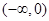 | B.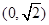 |
C.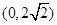 | D.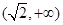 |
B
分析:由f(x)是偶函数,得f(2x-
 )=f(|2x-
)=f(|2x-  |),又f(x)在[0,+∞)上递增,得f(2x-
|),又f(x)在[0,+∞)上递增,得f(2x-  )<f(
)<f( )?|2x-
)?|2x-  |<
|< ,从而可解出x的范围.
,从而可解出x的范围.解:由题意得:f(2x-
 )<f(
)<f( )?f(|2x-
)?f(|2x- |)<f(
|)<f( )?|2x-
)?|2x- |<
|< ,解得0<x<
,解得0<x< .
.故x的取值范围为:(0,
 ).
).选B。

练习册系列答案
相关题目
题目内容
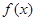 在区间
在区间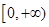 单调递增,
单调递增,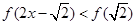 的
的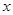 取值
取值A.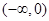 | B.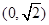 |
C.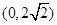 | D.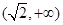 |
 )=f(|2x-
)=f(|2x-  |),又f(x)在[0,+∞)上递增,得f(2x-
|),又f(x)在[0,+∞)上递增,得f(2x-  )<f(
)<f( )?|2x-
)?|2x-  |<
|< ,从而可解出x的范围.
,从而可解出x的范围. )<f(
)<f( )?f(|2x-
)?f(|2x- |)<f(
|)<f( )?|2x-
)?|2x- |<
|< ,解得0<x<
,解得0<x< .
. ).
).