题目内容
【题目】如图,曲线C由上半椭圆C1: ![]() =1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为 ![]() .
. 
(1)求a,b的值;
(2)过点B的直线l与C1 , C2分别交于点P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.
【答案】
(1)解:在C1、C2的方程中,令y=0,可得b=1,且A(﹣1,0),B(1,0)是上半椭圆C1的左右顶点.
设C1:的半焦距为c,由 ![]() =
= ![]() 及a2﹣c2=b2=1得a=2.
及a2﹣c2=b2=1得a=2.
∴a=2,b=1.
(2)解:由(1)知上半椭圆C1的方程为 ![]() +x2=1(y≥0).
+x2=1(y≥0).
易知,直线l与x轴不重合也不垂直,设其方程为y=k(x﹣1)(k≠0),
代入C1的方程,整理得
(k2+4)x2﹣2k2x+k2﹣4=0.(*)
设点P(xp,yp),
∵直线l过点B,
∴x=1是方程(*)的一个根,
由求根公式,得xp= ![]() ,从而yp=
,从而yp= ![]() ,
,
∴点P的坐标为( ![]() ,
, ![]() ).
).
同理,由 ![]() 得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),
得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),
∴ ![]() =
= ![]() (k,﹣4),
(k,﹣4), ![]() =﹣k(1,k+2),
=﹣k(1,k+2),
∵AP⊥AQ,∴ ![]()
![]() =0,即
=0,即 ![]() [k﹣4(k+2)]=0,
[k﹣4(k+2)]=0,
∵k≠0,∴k﹣4(k+2)=0,解得k=﹣ ![]() .
.
经检验,k=﹣ ![]() 符合题意,
符合题意,
故直线l的方程为y=﹣ ![]() (x﹣1),即8x+3y﹣8=0.
(x﹣1),即8x+3y﹣8=0.
【解析】(1)在C1、C2的方程中,令y=0,即得b=1,设C1:的半焦距为c,由 ![]() =
= ![]() 及a2﹣c2=b2=1得a=2;(2)由(1)知上半椭圆C1的方程为
及a2﹣c2=b2=1得a=2;(2)由(1)知上半椭圆C1的方程为 ![]() +x2=1(y≥0),设其方程为y=k(x﹣1)(k≠0),代入C1的方程,整理得(k2+4)x2﹣2k2x+k2﹣4=0.(*)设点P(xp , yp),依题意,可求得点P的坐标为(
+x2=1(y≥0),设其方程为y=k(x﹣1)(k≠0),代入C1的方程,整理得(k2+4)x2﹣2k2x+k2﹣4=0.(*)设点P(xp , yp),依题意,可求得点P的坐标为( ![]() ,
, ![]() );同理可得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),利用
);同理可得点Q的坐标为(﹣k﹣1,﹣k2﹣2k),利用 ![]()
![]() =0,可求得k的值,从而可得答案.
=0,可求得k的值,从而可得答案.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.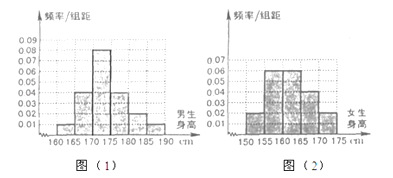
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
≥170cm | <170cm | 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:K2=![]()
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() 的数据作了初步统计,得到如下数据:
的数据作了初步统计,得到如下数据:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() ,即
,即![]() .对上述数据作了初步处理,得到相关的值如下表:
.对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值在区间
(万元)的比值在区间![]() 内时认为该年效益良好.该公司某
内时认为该年效益良好.该公司某![]() 年投入的宣传费用(单位:万元)分别为:
年投入的宣传费用(单位:万元)分别为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,试根据回归方程估计年销售量,从这
,试根据回归方程估计年销售量,从这![]() 年中任选
年中任选![]() 年,记其中选到效益良好年的数量为
年,记其中选到效益良好年的数量为![]() ,试求随机变量
,试求随机变量![]() 的分布列和期望.(其中
的分布列和期望.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.