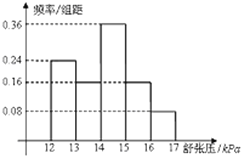
题目内容
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点. 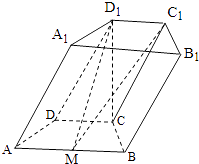
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ![]() ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
【答案】
(1)解:连接AD1,∵ABCD﹣A1B1C1D1为四棱柱,∴CD ![]() C1D1,
C1D1,
又M为AB的中点,∴AM=1.
∴CD∥AM,CD=AM,
∴AM ![]() C1D1,
C1D1,
∴AMC1D1为平行四边形,∴AD1∥MC1,又MC1平面A1ADD1,AD1平面A1ADD1,
∴C1M∥平面A1ADD1;
(2)解:解法一:∵AB∥A1B1,A1B1∥C1D1,
∴面D1C1M与ABC1D1共面,
作CN⊥AB,连接D1N,则∠D1NC即为所求二面角,
在ABCD中,DC=1,AB=2,∠DAB=60°,
∴CN= ![]() ,
,
在Rt△D1CN中,CD1= ![]() ,CN=
,CN= ![]() ,
,
∴D1N= ![]()
∴cos∠D1CN= ![]() =
= ![]() =
= ![]()
解法二:作CP⊥AB于P,以C为原点,CD为x轴,CP为y轴,CD1为z轴建立空间坐标系
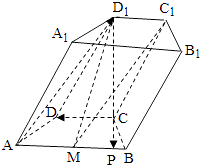
则C1(﹣1,0, ![]() ),D1,(0,0,
),D1,(0,0, ![]() ),M(
),M( ![]() ,
, ![]() ,0),
,0),
∴ ![]() =(1,0,0),
=(1,0,0), ![]() =(
=( ![]() ,
, ![]() ,﹣
,﹣ ![]() ),
),
设平面C1D1M的法向量 ![]() =(x1,y1,z1),
=(x1,y1,z1),
则 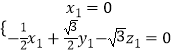 ,∴
,∴ ![]() =(0,2,1).
=(0,2,1).
显然平面ABCD的法向量 ![]() =(0,0,1),
=(0,0,1),
cos< ![]() ,
, ![]() >|=
>|= 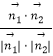 =
= ![]() =
= ![]() ,
,
显然二面角为锐角,
∴平面C1D1M和平面ABCD所成的角(锐角)的余弦值为 ![]() .
.
【解析】(1)连接AD1 , 易证AMC1D1为平行四边形,利用线面平行的判定定理即可证得C1M∥平面A1ADD1;(2)作CP⊥AB于P,以C为原点,CD为x轴,CP为y轴,CD1为z轴建立空间坐标系,易求C1(﹣1,0, ![]() ),D1 , (0,0,
),D1 , (0,0, ![]() ),M(
),M( ![]() ,
, ![]() ,0),
,0), ![]() =(1,1,0),
=(1,1,0), ![]() =(
=( ![]() ,
, ![]() ,﹣
,﹣ ![]() ),设平面C1D1M的法向量
),设平面C1D1M的法向量 ![]() =(x1 , y1 , z1),可求得
=(x1 , y1 , z1),可求得 ![]() =(0,2,1),而平面ABCD的法向量
=(0,2,1),而平面ABCD的法向量 ![]() =(1,0,0),从而可求得平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
=(1,0,0),从而可求得平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 名校课堂系列答案
名校课堂系列答案