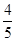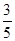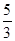题目内容
已知椭圆
+
=1(a>b>0)的离心率为
,长轴长为2
,直线l:y=kx+m交椭圆于不同的两点A,B.
(Ⅰ)求椭圆的方程;
(Ⅱ)若m=1,且
•
=0,求k的值(O点为坐标原点);
(Ⅲ)若坐标原点O到直线l的距离为
,求△AOB面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 3 |
(Ⅰ)求椭圆的方程;
(Ⅱ)若m=1,且
| OA |
| OB |
(Ⅲ)若坐标原点O到直线l的距离为
| ||
| 2 |
(Ⅰ)设椭圆的半焦距为c(c>0),依题意
解得c=
.
由a2=b2+c2,得b=1.
∴所求椭圆方程为
+y2=1
(Ⅱ)∵m=1,∴y=kx+1.
设A(x1,y1),B(x2,y2),其坐标满足方程
消去y并整理得(1+3k2)x2+6kx=0&,
则△=(6k)2-4(1+3k2)×0>0&,解得k≠0.
故x1+x2=
,x1•x2=0.
∵
•
=0,∴x1x2+y1y2=x1x2+(kx1+1)•(kx2+1)=(1+k2)x1x2+k(x1+x2)+1
=(1+k2)×0+k•
+1=
=0∴k=±
.
(Ⅲ)由已知
=
,可得m2=
(k2+1).
将y=kx+m代入椭圆方程,整理得(1+3k2)x2+6kmx+3m2-3=0.
△=(6km)2-4(1+3k2)(3m2-3)>0(*)
∴x1+x2=
,x1•x2=
.
∴|AB|2=(1+k2)(x2-x1)2=(1+k2)[
-
]
=
=
=3+
=3+
≤3+
=4(k≠0).
当且仅当9k2=
,即k=±
时等号成立.
经检验,k=±
满足(*)式.
当k=0时,|AB|=
.
综上可知|AB|max=2.∴当|AB|最大时,△AOB的面积取最大值S=
×2×
=
.
|
| 2 |
由a2=b2+c2,得b=1.
∴所求椭圆方程为
| x2 |
| 3 |
(Ⅱ)∵m=1,∴y=kx+1.
设A(x1,y1),B(x2,y2),其坐标满足方程
|
则△=(6k)2-4(1+3k2)×0>0&,解得k≠0.
故x1+x2=
| -6k |
| 1+3k2 |
∵
| OA |
| OB |
=(1+k2)×0+k•
| -6k |
| 1+3k2 |
| 1-3k2 |
| 3k2+1 |
| ||
| 3 |
(Ⅲ)由已知
| |m| | ||
|
| ||
| 2 |
| 3 |
| 4 |
将y=kx+m代入椭圆方程,整理得(1+3k2)x2+6kmx+3m2-3=0.
△=(6km)2-4(1+3k2)(3m2-3)>0(*)
∴x1+x2=
| -6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
∴|AB|2=(1+k2)(x2-x1)2=(1+k2)[
| 36k2m2 |
| (3k2+1)2 |
| 12(m2-1) |
| 3k2+1 |
=
| 12(k2+1)(3k2+1-m2) |
| (3k2+1)2 |
| 3(k2+1)(9k2+1) |
| (3k2+1)2 |
=3+
| 12k2 |
| 9k4+6k2+1 |
| 12 | ||
9k2+
|
| 12 |
| 2×3+6 |
当且仅当9k2=
| 1 |
| k2 |
| ||
| 3 |
经检验,k=±
| ||
| 3 |
当k=0时,|AB|=
| 3 |
综上可知|AB|max=2.∴当|AB|最大时,△AOB的面积取最大值S=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
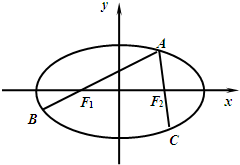
 中,已知中心在坐标原点的双曲线
中,已知中心在坐标原点的双曲线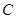 经过点
经过点 ,且它的右焦点
,且它的右焦点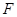 与抛物线
与抛物线 的焦点相同,则该双曲线的标准方程为 .
的焦点相同,则该双曲线的标准方程为 .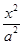 -
- =1(a>0,b>0)的左,右焦点,若在双曲线右支上存在一点P,满足|PF2|=|F1F2|,且点F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率e为( )
=1(a>0,b>0)的左,右焦点,若在双曲线右支上存在一点P,满足|PF2|=|F1F2|,且点F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率e为( )