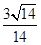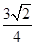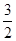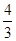题目内容

椭圆
x2
a2
+
y2
b2
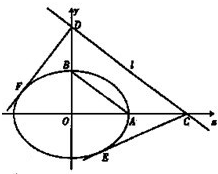
=1（a＞b＞0）的一个焦点为F1，若椭圆上存在一个点P，满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点，则椭圆的离心率为______．
设以椭圆的短轴为直径的圆与线段PF1相切于点M，连结OM、PF2，
∵M、O分别为PF1、F1F2的中点，
∴MO∥PF2，且|PF2|=2|MO|=2b，
又∵线段PF1与圆O相切于点M，可得OM⊥PF1，
∴PF1⊥PF2，
∴|PF1|=
4c2-4b2
=2
c2-b2
．
∴|PF1|+|PF2|=2
c2-b2
+2b=2a，
化简得2ab=a2-c2+2b2=3b2，
∴b=
2
3
a，c=
5
3
a，
∴离心率为e=
c
a
=
5
3
．
故答案为：
5
3
．
练习册系列答案
相关题目
已知两点A（-1，0），B（1，0），且点C（x，y）满足
(x-1)2+y2
|x-4|
=
1
2
，则|AC|+|BC|=（　　）
A．6B．2C．4D．不能确定
如图，已知A，B分别为椭圆
x2
a2
+
y2
b2
=1(a＞b＞)的右顶点和上顶点，直线 l∥AB，l与x轴、y轴分别交于C，D两点，直线CE，DF为椭圆的切线，则CE与DF的斜率之积kCE•kDF等于（　　）
A．±
a2
b2
B．±
a2-b2
a2
C．±
b2
a2
D．±
a2-b2
b2
已知F1，F2分别是椭圆的左，右焦点，现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M，N，若过F1的直线MF1是圆F2的切线，则椭圆的离心率为（　　）
A．
3
-1		B．2-
3
C．
2
2
D．
3
2
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
6
3
，长轴长为2
3
，直线l：y=kx+m交椭圆于不同的两点A，B．
（Ⅰ）求椭圆的方程；
（Ⅱ）若m=1，且
OA
•
OB
=0，求k的值（O点为坐标原点）；
（Ⅲ）若坐标原点O到直线l的距离为
3
2
，求△AOB面积的最大值．
设P为椭圆
x2
16
+
y2
9
=1上的动点，则P到直线x+y-6=0的最小距离为（　　）
A．1B．2C．
2
2
D．
2
以知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的两个焦点分别为F1（-c，0）和F2（c，0）（c＞0），过点E(
a2
c
，0)的直线与椭圆相交于A，B两点，且F1A∥F2B，|F1A|=2|F2B|．
（1）求椭圆的离心率；
（2）求直线AB的斜率；
（3）设点C与点A关于坐标原点对称，直线F2B上有一点H（m，n）（m≠0）在△AF1C的外接圆上，求
n
m
的值．
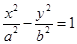已知双曲线C：（a>b>0)的一个焦点为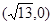，离心率为.
（1）求双曲线C的标准方程；
（2）若动点P(x0,y0)为双曲线外一点，且点P到双曲线C的两条切线相互垂直，求点P的轨迹方程。
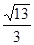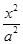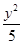已知双曲线－＝1的右焦点为(3,0)，则该双曲线的离心率等于(　　)
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网