题目内容
设 分别为椭圆
分别为椭圆 的左、右两个焦点,若椭圆C上的点A(1,
的左、右两个焦点,若椭圆C上的点A(1, )到F1,F2两点的距离之和等于4.
)到F1,F2两点的距离之和等于4.
(1)写出椭圆C的方程和焦点坐标;
(2)过点P(1, )的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
)的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
(3)过点Q(1,0)的直线与椭圆交于两点M、N,若△OMN面积取得最大,求直线MN的方程.
 分别为椭圆
分别为椭圆 的左、右两个焦点,若椭圆C上的点A(1,
的左、右两个焦点,若椭圆C上的点A(1, )到F1,F2两点的距离之和等于4.
)到F1,F2两点的距离之和等于4.(1)写出椭圆C的方程和焦点坐标;
(2)过点P(1,
 )的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
)的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;(3)过点Q(1,0)的直线与椭圆交于两点M、N,若△OMN面积取得最大,求直线MN的方程.
(1)椭圆C的方程为
(2)4x+4y=5
(3)x=1

(2)4x+4y=5
(3)x=1
(1)椭圆C的焦点在x轴上,
由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2.;
又点A(1, ) 在椭圆上,因此
) 在椭圆上,因此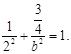 得b2=1,于是c2=3;
得b2=1,于是c2=3;
所以椭圆C的方程为 ,
,
(2)∵P在椭圆内,∴直线DE与椭圆相交,
∴设D(x1,y1),E(x2,y2),代入椭圆C的方程得
x12+4y12-4="0," x22+4y22-4=0,相减得2(x1-x2)+4×2× (y1-y2)=0,∴斜率为k=-1
(y1-y2)=0,∴斜率为k=-1
∴DE方程为y-1= -1(x- ),即4x+4y=5;
),即4x+4y=5;
(3)直线MN不与y轴垂直,∴设MN方程为my=x-1,代入椭圆C的方程得
(m2+4)y2+2my-3="0," 设M(x1,y1),N(x2,y2),则y1+y2=-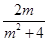 , y1y2=-
, y1y2=- ,且△>0成立.
,且△>0成立.
又S△OMN=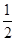 |y1-y2|=
|y1-y2|=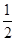 ×
×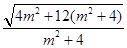 =
=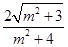 ,设t=
,设t= ≥
≥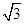 ,则
,则
S△OMN=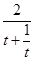 ,(t+
,(t+ )′=1-t-2>0对t≥
)′=1-t-2>0对t≥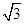 恒成立,∴t=
恒成立,∴t=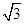 时t+
时t+ 取得最小,S△OMN最大,
取得最小,S△OMN最大,
此时m=0,∴MN方程为x=1
由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2.;
又点A(1,
 ) 在椭圆上,因此
) 在椭圆上,因此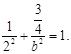 得b2=1,于是c2=3;
得b2=1,于是c2=3;所以椭圆C的方程为
 ,
,(2)∵P在椭圆内,∴直线DE与椭圆相交,
∴设D(x1,y1),E(x2,y2),代入椭圆C的方程得
x12+4y12-4="0," x22+4y22-4=0,相减得2(x1-x2)+4×2×
 (y1-y2)=0,∴斜率为k=-1
(y1-y2)=0,∴斜率为k=-1∴DE方程为y-1= -1(x-
 ),即4x+4y=5;
),即4x+4y=5;(3)直线MN不与y轴垂直,∴设MN方程为my=x-1,代入椭圆C的方程得
(m2+4)y2+2my-3="0," 设M(x1,y1),N(x2,y2),则y1+y2=-
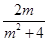 , y1y2=-
, y1y2=- ,且△>0成立.
,且△>0成立.又S△OMN=
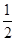 |y1-y2|=
|y1-y2|=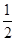 ×
×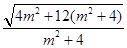 =
=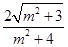 ,设t=
,设t= ≥
≥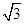 ,则
,则S△OMN=
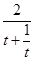 ,(t+
,(t+ )′=1-t-2>0对t≥
)′=1-t-2>0对t≥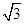 恒成立,∴t=
恒成立,∴t=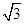 时t+
时t+ 取得最小,S△OMN最大,
取得最小,S△OMN最大,此时m=0,∴MN方程为x=1

练习册系列答案
相关题目
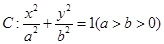 的两个焦点分别为
的两个焦点分别为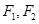 ,且
,且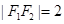 ,点
,点 在椭圆上,且
在椭圆上,且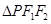 的周长为6.
的周长为6. 的方程;(2)若点
的方程;(2)若点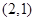 ,不过原点
,不过原点 的直线
的直线 与椭圆
与椭圆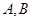 不同两点,设线段
不同两点,设线段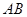 的中点为
的中点为 ,且
,且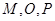 三点共线.设点
三点共线.设点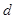 ,求
,求 的焦点在
的焦点在 轴上,
轴上,  分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点 是椭圆在第一象限内的点,直线
是椭圆在第一象限内的点,直线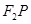 交
交 轴于点
轴于点 ,
, 时,
时, 的离心率为
的离心率为 ,求椭圆
,求椭圆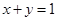 上时,求直线
上时,求直线 与
与 的夹角;
的夹角; 时,若总有
时,若总有 ,猜想:当
,猜想:当 变化时,点
变化时,点 是否在某定直线上,若是写出该直线方程(不必求解过程).
是否在某定直线上,若是写出该直线方程(不必求解过程).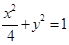 的弦
的弦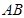 的中点为
的中点为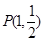 ,则弦
,则弦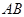 所在直线的方程是 .
所在直线的方程是 .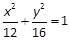 ,则以点
,则以点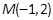 为中点的弦所在直线方程为( ).
为中点的弦所在直线方程为( ).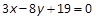
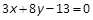
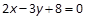
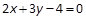
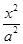 +
+ =1(a>b>0)的左顶点为A,左、右焦点分别为F1,F2,D是它短轴上的一个端点,若3
=1(a>b>0)的左顶点为A,左、右焦点分别为F1,F2,D是它短轴上的一个端点,若3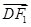 =
=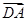 +2
+2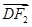 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )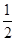

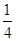
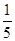
 :
: ,过点
,过点
 的直线与椭圆
的直线与椭圆 、
、 两点,若点
两点,若点 的中点,则直线
的中点,则直线