题目内容
已知数列{an}中,a1= ,an=2-
,an=2-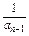 (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn= (n∈N*).
(n∈N*).
(1)求证:数列{bn}是等差数列;
(2)求数列{an}中的最大项和最小项,并说明理由.
 ,an=2-
,an=2-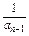 (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn= (n∈N*).
(n∈N*).(1)求证:数列{bn}是等差数列;
(2)求数列{an}中的最大项和最小项,并说明理由.
(1)证明见解析(2)当n=3时,an取得最小值-1;当n=4时,an取得最大值3.
(1)证明 因为an=2-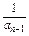 (n≥2,n∈N*),bn=
(n≥2,n∈N*),bn= .
.
所以当n≥2时,bn-bn-1= -
-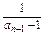
=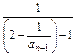 -
- =
=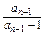 -
-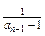 =1.
=1.
又b1=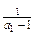 =-
=-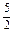 .所以,数列{bn}是以-
.所以,数列{bn}是以-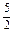 为首项,以1为公差的等差数列.
为首项,以1为公差的等差数列.
(2)解 由(1)知,bn=n- ,则an=1+
,则an=1+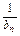 =1+
=1+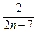 .
.
设函数f(x)=1+ ,易知f(x)在区间(-∞,
,易知f(x)在区间(-∞,  )和(
)和( ,+∞)内为减函数.
,+∞)内为减函数.
所以,当n=3时,an取得最小值-1;当n=4时,an取得最大值3.
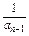 (n≥2,n∈N*),bn=
(n≥2,n∈N*),bn= .
.所以当n≥2时,bn-bn-1=
 -
-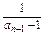
=
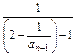 -
- =
=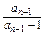 -
-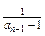 =1.
=1.又b1=
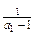 =-
=-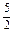 .所以,数列{bn}是以-
.所以,数列{bn}是以-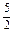 为首项,以1为公差的等差数列.
为首项,以1为公差的等差数列.(2)解 由(1)知,bn=n-
 ,则an=1+
,则an=1+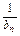 =1+
=1+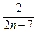 .
.设函数f(x)=1+
 ,易知f(x)在区间(-∞,
,易知f(x)在区间(-∞,  )和(
)和( ,+∞)内为减函数.
,+∞)内为减函数.所以,当n=3时,an取得最小值-1;当n=4时,an取得最大值3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
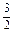 f(bn-1) (n∈N,n≥2),求证:
f(bn-1) (n∈N,n≥2),求证: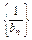 为等差数列,并求bn.
为等差数列,并求bn. 时,求Sn.
时,求Sn.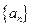 的前
的前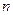 项和为
项和为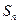 ,已知对任意正整数
,已知对任意正整数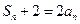 成立。
成立。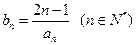 ,数列
,数列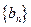 的前
的前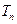 ,求证:
,求证: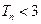 。
。 是一次函数,且
是一次函数,且 ,
, ,其中
,其中 自然对数的底。(1)求函数
自然对数的底。(1)求函数 中,
中, ,
, ,求数列
,求数列 满足
满足 ,试求数列
,试求数列 项和
项和 。
。 的前n项和,求Tn.
的前n项和,求Tn.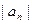 满足:
满足: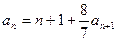 ,且存在大于1的整数k使
,且存在大于1的整数k使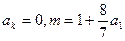 。
。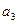 表示m(不必化简)
表示m(不必化简)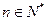 ,点(n,Sn)总在抛物线y=ax2+bx+c
,点(n,Sn)总在抛物线y=ax2+bx+c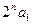 +
+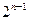 a2+
a2+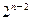 a3+…+
a3+…+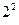
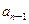 +2
+2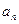 .
.