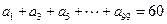题目内容
数列{an}是首项a1=4的等比数列，且S3，S2，S4成等差数列.
（1）求数列{an}的通项公式；
（2）设bn=log2|an|,Tn为数列
的前n项和，求Tn.
（1）求数列{an}的通项公式；
（2）设bn=log2|an|,Tn为数列
的前n项和，求Tn.（1）an=4(-2)n-1=(-2)n+1（2）
-
=
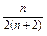
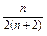
-=（1）当q=1时，S3=12，S2=8，S4=16，不成等差数列.
q≠1时，
=
+
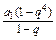
得2q2=q3+q4,∴q2+q-2=0,∴q=-2.
∴an=4(-2)n-1=(-2)n+1.
(2)bn=log2|an|=log2|(-2)n+1|=n+1.
=
=
-
∴Tn=
+
+…+
=-=.
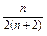q≠1时，
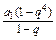
=+得2q2=q3+q4,∴q2+q-2=0,∴q=-2.
∴an=4(-2)n-1=(-2)n+1.
(2)bn=log2|an|=log2|(-2)n+1|=n+1.
==-∴Tn=
++…+=
-=.
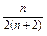练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
，an=2-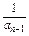
(n≥2,n∈N*),数列{bn}满足bn=
(n∈N*).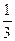
,a2+a5=4,an=33,则n为___________________.
为整数，集合
中的数由小到大组成数列
：
，则
。
+
+
+…+
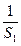的值为?多少？
