题目内容
设数列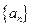 的前
的前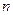 项和为
项和为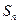 ,已知对任意正整数
,已知对任意正整数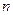 ,都有
,都有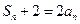 成立。
成立。
(I)求数列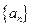 的通项公式;
的通项公式;
(II)设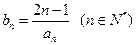 ,数列
,数列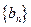 的前
的前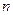 项和为
项和为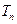 ,求证:
,求证: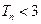 。
。
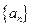 的前
的前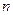 项和为
项和为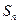 ,已知对任意正整数
,已知对任意正整数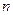 ,都有
,都有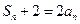 成立。
成立。(I)求数列
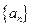 的通项公式;
的通项公式;(II)设
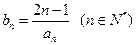 ,数列
,数列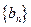 的前
的前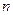 项和为
项和为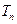 ,求证:
,求证: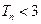 。
。(I)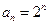
(II)证明见解析。
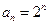
(II)证明见解析。
(I)当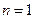 时,
时,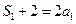 ,所以
,所以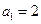 。 (2分)
。 (2分)
因为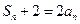 ,则
,则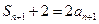 ,两式相减,得
,两式相减,得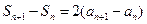 ,
,
即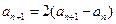 ,即
,即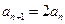 。 (4分)
。 (4分)
所以数列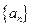 是首项为2,公比为2的等比数列,故
是首项为2,公比为2的等比数列,故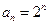 。 (6分)
。 (6分)
(II)因为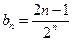 ,则
,则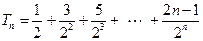 。 ① (7分)
。 ① (7分)
所以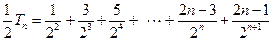 。 ② (8分)
。 ② (8分)
①-②,得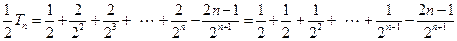
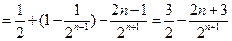 。 (10分)
。 (10分)
所以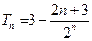 .因为
.因为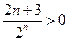 ,故
,故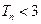 。 (12分)
。 (12分)
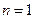 时,
时,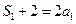 ,所以
,所以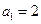 。 (2分)
。 (2分)因为
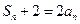 ,则
,则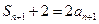 ,两式相减,得
,两式相减,得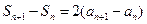 ,
,即
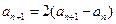 ,即
,即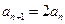 。 (4分)
。 (4分)所以数列
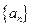 是首项为2,公比为2的等比数列,故
是首项为2,公比为2的等比数列,故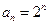 。 (6分)
。 (6分)(II)因为
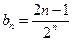 ,则
,则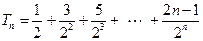 。 ① (7分)
。 ① (7分)所以
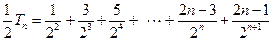 。 ② (8分)
。 ② (8分)①-②,得
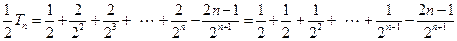
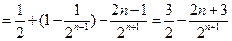 。 (10分)
。 (10分)所以
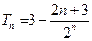 .因为
.因为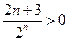 ,故
,故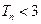 。 (12分)
。 (12分)
练习册系列答案
相关题目
 ,an=2-
,an=2-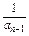 (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn= (n∈N*).
(n∈N*).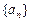 、
、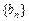 、
、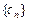 满足:
满足: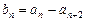 ,
,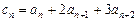 (n=1,2,3,…), 证明:
(n=1,2,3,…), 证明: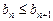 (n=1,2,3,…)
(n=1,2,3,…)



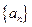 满足,
满足,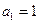 ,
,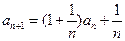 (n∈N*)。
(n∈N*)。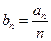 ,求数列
,求数列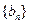 的通项公式;
的通项公式; ,求证:当正整数n≥2时,an+1<an。
,求证:当正整数n≥2时,an+1<an。 !=(n
!=(n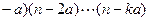 ,其中k是满足n>ka的最大整数,那么
,其中k是满足n>ka的最大整数,那么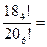 _________
_________