题目内容
设数列{an}的前n项和为Sn，且（3-m）Sn+2man="m+3" （n∈N*），其中m为常数，且m≠-3,m≠0.
（1）求证：{an}是等比数列；
（2）若数列{an}的公比q=f(m),数列{bn}满足b1=a1,bn=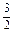
f(bn-1) (n∈N,n≥2),求证：
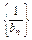为等差数列，并求bn.
（1）求证：{an}是等比数列；
（2）若数列{an}的公比q=f(m),数列{bn}满足b1=a1,bn=
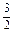f(bn-1) (n∈N,n≥2),求证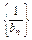：为等差数列，并求bn.（1）证明见解析（2）证明见解析
证明 （1）由(3-m)Sn+2man=m+3,
得(3-m)Sn+1+2man+1=m+3,
两式相减，得（3+m）an+1=2man,m≠-3,
∴
=
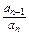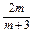≠0 (n≥1).∴{an}是等比数列.
（2）由(3-m)S1+2ma1=m+3,解出a1=1,∴b1=1.
q="f(m)="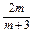,n∈N且n≥2时，
bn=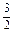f(bn-1)= ·
，
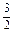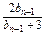bnbn-1+3bn=3bn-1，推出
-
=
.
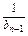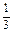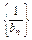∴是以1为首项、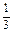为公差的等差数列.
∴=1+
=
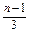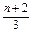.∴bn=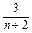
.
得(3-m)Sn+1+2man+1=m+3,
两式相减，得（3+m）an+1=2man,m≠-3,
∴
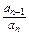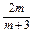=≠0 (n≥1).∴{an}是等比数列.（2）由(3-m)S1+2ma1=m+3,解出a1=1,∴b1=1.
q="f(m)="
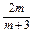,n∈N且n≥2时，bn=
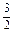f(bn-1)= 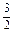·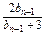，bnbn-1+3bn=3bn-1，推出
-=.∴
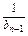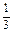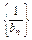是以1为首项、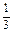为公差的等差数列.∴
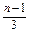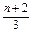=1+=.∴bn=.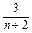
练习册系列答案
津桥教育计算小状元系列答案
相关题目
，an=2-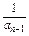
(n≥2,n∈N*),数列{bn}满足bn=
(n∈N*).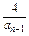
(n≥2),令bn=
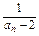.求证：数列{bn}是等差数列.
，试问当n为何值时，
最大？并求出
为整数，集合
中的数由小到大组成数列
：
，则
。
+
+
+…+
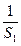的值为?多少？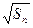
=an+1.
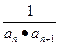,求数列{bn}的前n项和Bn.
!=(n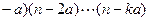
，其中k是满足n>ka的最大整数，那么
_________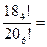